Elementary Math K-8
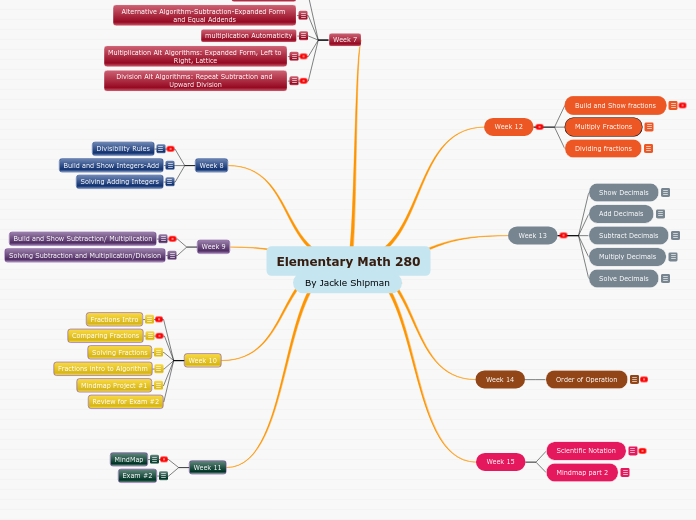
Week 9
Practice solving fractions in class and talk bout the exam
Week 8
Prime Factorization
Every composite number has its own “fingerprint” or “DNA” which is made of prime numbers multiplied together. That fingerprint is called the prime factorization of the number
The List Method:
-The factors of 24 are: 1, 2, 3, 4, 6, 8, 12 and 24
The factors of 36 are: 1, 2, 3, 4, 6, 9, 12, 18 and 36
24 and 36 have many common factors. The greatest common factor, however is 12. So the GCF of 24 and 36 is 12.
-The multiples of 24 are: 0, 24, 48, 72, 96, ...
The multiples of 36 are: 0, 36, 72, 108, ...
The least common nonzero multiple is 72. So the LCM of 24 and 36 is 72
The Prime Factorization Method:
- The prime factorization of 24 is: 24= 2 x 2 x 2 x 3
The prime factorization of 36 is: 36= 2 x 2 x 3 x 3
Look at both lists. If you see a number they have in common, write it down. The common numbers here are 2, 2, and 3
To find the GCF multiply the common numbers: 2x2x3=12
To find the LCM multiply the GCF by the numbers that haven’t been
used. The LCM is 12x2x3=72
Fractions
Three meaning of Fractions:
1. Part-Whole: This is the most common understanding of fraction. A fraction such as ¾ represents a whole which has been partitioned into 4 equal parts and 3 of these parts are being considered.
2. Quotient: This meaning comes from division; 3:5=3/5
3. Ratio: This meaning is conceptually different than the other two. Part/part ratio is NOT a fraction. Part/Whole ratio is a fraction
Reasoning Strategies for comparing fractions
1. Same-sized parts (same denominator)
5/10 is greater than 3/10
2. Same number but different-sized parts (same numerators)
2/5 is greater than 2/9
3. More/less than one-half or one whole (comparison to benchmarks)
7/8 is less than 8/7
3/7 is less than 5/8
4. Closeness to one-half or one whole (distance from benchmarks)
3/4 is greater than 9/10
Week 7
Main topic
Week 7 we learned about Disability rules:
Divisible: a is divisible by b, if there is a number c that meets this requirements: bxc=a (10 is divisible by 5 because there is a number, the number 2, that meets the requirement 2x5=10
•10 is divisible by 5
•5 is a divisor of 10
•5 is a factor of 10
•10 is a multiple of 5
A number is divisible by a second number if the second number divides into the first number with no remainder.
- A number is divisible by 2 if it ends in 0, 2, 4, 6, or 8
-A number is divided by 3 if the sum of its digits is also divided
by 3
Ex. 543: 5+4+3=12. Since 12 is divisible by 3, so is 543
- A number is divisible by 4 if the last two digits of the number
are divisible by 4
-A number is divisible by 5 if it ends in 5 or 0
-A number is divisible by 6 if it is divisible by BOTH 2 and 3
- A number is divisible by 8 if the last three digits are divisible by 8 (not a very
helpful rule!)
-A number is divisible by 9 if the sum of its digits is divisible by 9
-A number is divisible by 10 if it ends in 0
- A number is divisible by 7 if the following rule works:
Double the last digit and subtract it from the remaining number. If the result is
divisible by 7, so is the original number. Apply this rule as many times as needed.
main topic pt 2
Prime, Composite and Identity Numbers
- A prime number has exactly two factors: one and itself
The prime numbers through 60 are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59. please not that 1 is NOT a prime number because it has only one factor, itself.
-A composite number is a number with more than two factors
- Zero and one are very special numbers in our number system:
0 is called the Additive identity element
1 is called the Multiplicative identity element
*Zero and one are neither prime nor composite
Week 6
Subtopic
Week 6 we took the test and went over it.
Week 5
Week 5: Multiplication Algorithms "repeated addiction"
Properties:
Identity: ax1=a
Zero: ax0=0
Order: axb=bxa
Commutative: 3x8=8x3
Associative "grouping": (axb)xc=ax(bxc)
1.) Standard ALG
2.) Place value
3.) Expanded notation
4.) Lattice ALG
Division Algorithms:" repeated subtraction"
1.) Standard Division ALG
2.) Emphasis Division ALG
3.) Alternate DivisionALG
• Compatible Numbers: To find 105 ÷ 3 we look for two numbers that are divisible by 3 and whose sum is 105, namely, 90 and 15. We then divide both numbers by 3 to obtain 90 ÷ 3 = 30 and 15 ÷ 3=5. Finally add the quotients to obtain 105 ÷ 3 = 30 + 5 = 35.
Week 4
Week 4: Addition Algorithms:
1.) Standard American ALG
2.)Partial Sums ALG
3.)Partial Sums with Emphasis on place Value
4.)Left-to- right ALG
5.) Expanded Notation ALG
6.)Lattice ALG
• Left-to-Right Approach (Front End Addition): In this model, to add 347 and 129, we first add the hundreds (300 + 100) then the tens (40 + 20), and then the ones (7+9), to obtain 476.
• Compensation: To find the sum 67 + 29, we add 67 + 30 (since 30 is the next multiple of 10 greater than 29) to obtain 97 and then we subtract 1 from 97 to compensate for the extra 1 that was added to obtain
97−1 = 96.
• Using Compatible Numbers: Compatible numbers are numbers whose sums are easy to calculate mentally. For example, if we are trying to find the sum 130 + 50 + 70 + 20 + 50 we will add first the numbers 130 and 70 to obtain 200, the numbers 50 and 50 to obtain 100, then the numbers 200 and 100 to obtain 300 and finally we add 20 to 300 to obtain 320.
• Breaking Up and Bridging: To find the sum 67 + 36 we find first the sum 67 + 30 = 97 and then the sum 97 + 6 = 103.
Subtraction Algorithms:
1.) American Stand ALG
2.) European-Mexican ALG
3.)Reverse Indian ALG
4.)Left-to-Right ALG
5.)Expanded Notation ALG
6.)Integer Subtraction ALG
• Left-to-Right: To find the difference 93 − 38 we find first 90 − 30 = 60, then 8 −3 = 5 and finally 60 − 5 = 55. To find the difference, 47 −32, we find first 40 − 30 = 10, then 7 −2 = 5 and
finally 10 + 5 = 15.
• Breaking Up and Bridging: To find the difference 67 − 36 we first find 67 − 30 = 37 and then 37 −6 = 31.
• Compensation: To find 47−29 is the same as finding 48−30= 18. That is we add the same number to both addends. This is known as the equal addition method for subtraction.
• Drop the Zeros: To find 8700 − 500 we find 87 −5 = 82 and then add the two zeros to the right of 82 to obtain 8200.
• Compatible Numbers: To find the difference 170 − 50 − 30 − 50 we can find first 170 − 30 = 140, then 50 + 50 = 100 and finally 140 −100 =
Week 3
Topic: Numeration Systems
Numerations systems have been developed over the centuries as a way of recording quantity.
Some number systems are positional which means that the placement of
digits (or numerals) in the number specifies the value of the number. An example of such a number system is the decimal system that we use(Base-10)
Our System: Base-10/Decimal
The number system we use in our schools and society is the Base-10 system. There is a consistent one-to-ten relationship between the digits of any number in the Base-10 system.
Digits used
•In Base-10: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
•In Base-2: 0, 1
•In Base-3: 0, 1, 2
•In Base-4: 0, 1, 3
•In Base-5: 0, 1, 2, 3, 4
Expanded Notation
It is very important that we understand place value and expanded notation very well, as well as powers of ten. They are very important concepts that we teach our students in elementary and middle school.
Expanded notation:
723=700+20+3
723=(7x100)+(2x10)+(3x1)
723=(7x10^2)+(2x10^1)+(3x10^0)
Week 2
Topic: Problem solving
Polya’s Four Steps to Problem Solving
1.Understand the problem
2.Devise a plan
3.Carry out the plan
4. Reflect
Make sure to understand the problem if your plan does not work then find another way to solve the problem.
Week 1
Introduction to the course, reviewing syllabus.