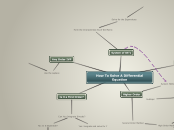
How To Solve A Differential Equation

Lisää tämän kaltaisia

Math2250

luonut jordan wu

Differential Equations

luonut adam terry

Differential equations

luonut Cameron Coombs

Differential Equations

luonut Luke Berhold

How To Solve A Differential Equation

Higher Order

Second Order Method

High Order Method

Homogeneous

System Method

System of DE's

Form the Characteristic Eq of the Matrix

Solve for the Eigenvalues

Plug in those Eigenvalues

Obatin Eigenvectors

Form the General Solution

Second Order?

Homogeneous?

Form The Characteristic Equation

Using the C.E's, Find its roots

Complex Imaginary Roots

Solution: y(t)=e^(At)(c1cosBt+c2sinBt)

Repeated Roots

Solution: y(t)=c1e^(r1t)+c2te^(r1t)

Real Roots

Solution: y(t)=c1e^(r1t)+c2e^(r2t)

Non-Homogeneous

Subtopic

First, Find the Homogenous Solution

Then Find the Particular Solution

Variation of Parameters Method

Undetermined Coefficeint Method

Any Order IVP

Use the Laplace

Solve for Y

Take the Inverse of the Laplace

Is it a First Order?

Can You Integrate Directly?

No: Is it Seperable?

Seperable?

No: Can you use the Integrating Factor Method?

Integrating Factor Method

What is the Integrating Factor?

Multiply by the Integrating Factor

Finally, Solve for Y

Yes: Integrate and solve for Y

Yes: Inegrate and solve for Y