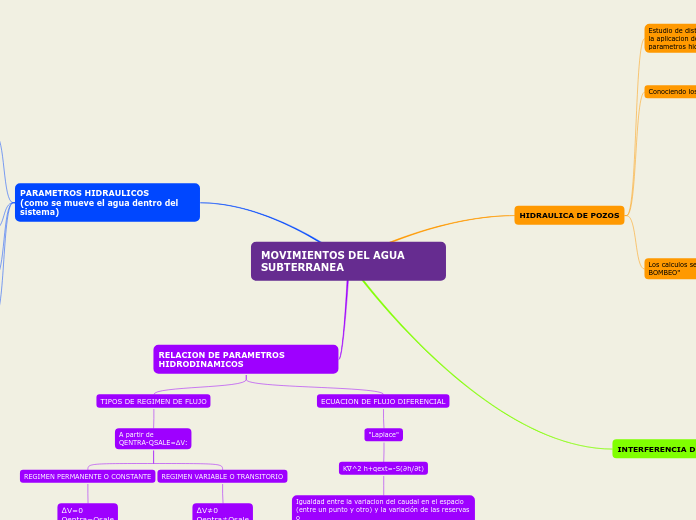
MOVIMIENTOS DEL AGUA SUBTERRANEA

Lisää tämän kaltaisia

Robitica

luonut Jorge Gonzalez

Organigrama

luonut Jose Manuel Moreno

CATETERISMO VESICAL- PROCESO

luonut Ginger Lisbeth Azanza Atariguana

propiedades fisicas y quimicas de la arcilla

luonut EVELIN LIZARAZO

MOVIMIENTOS DEL AGUA SUBTERRANEA

RELACION DE PARAMETROS HIDRODINAMICOS

ECUACION DE FLUJO DIFERENCIAL

"Laplace"

K∇^2 h+qext=-S(∂h/∂t)

Igualdad entre la variacion del caudal en el espacio (entre un punto y otro) y la variación de las reservas o almacenamiento del sistema en el tiempo.

TIPOS DE REGIMEN DE FLUJO

A partir de QENTRA-QSALE=∆V:

REGIMEN VARIABLE O TRANSITORIO

∆V≠0 Qentra≠Qsale

REGIMEN PERMANENTE O CONSTANTE

∆V=0 Qentra=Qsale

PARAMETROS HIDRAULICOS (como se mueve el agua dentro del sistema)

COEFICIENTE DE ALMACENAMIENTO (S)

Volumen de agua que un acuífero acepta o cede dentro de un prisma cuya base es unitaria y con una altura igual al espesor del acuífero cuando desciende o eleva el nivel piezométrico en una unidad

TRANSMISIBILIDAD (T)

Es el caudal filtrado a través de una faja vertical, de ancho igual a la unidad, y con una altura igual a la del manto saturado, bajo un gradiente hidráulico unitario

PERMEABILIDAD (k)

Obtenida por LEY DE DARCY: q=-k/μ*∆P q: caudal k: permeabilidad μ: viscosidad ∆P: bajada de presión

Facilidad que posee el fluido para atravesar determinada formación geológica

POROSIDAD

Coeficiente de relacion especifica

Es aquel volumen de agua, que luego de drenarla por gravedad (Vg), queda en la muestra del suelo

Porosidad por fracturacion

Mas bien conocida como porosidad secundaria, es aquella que se produce posteriormente del origen de la formación geológica

Porosidad eficaz

Relaciona el Volumen de agua que contiene los poros interconectados y que se mueve por gravedad (Vg) y el volumen del suelo (V) p= Vg/V

Porosidad total

Relación entre volumen de huecos (Vh) con respecto al volumen del suelo o roca (V) p= Vh/V

INTERFERENCIA DE POZOS

dT=0,183/T[Q1 log⁡(2,25Tt/(〖r1〗^2 S))+Q2 log⁡(2,25Tt/(〖r2〗^2 S))]

La interferencia de perforaciones de agua subterránea se puede expresar como la influencia que tiene una perforación sobre otra, de modo que los conos de depresión.

HIDRAULICA DE POZOS

Los calculos se obtienen por el "ENSAYO DE BOMBEO"

REGIMEN VARIABLE

ECUACION DE JACOB

d=Q/4πT W_((u))=Q/4πT ln( 2,25Tt/(r^2 S))

REGIMEN PERMANENTE

ECUACIONES DUPUIT-THIEM

ACUIFERO LIBRE

d1-d2=Q/(2πKh_0 ) ln( r2/r1)

ACUIFERO CONFINADO

d1=Q/2πbK ln (R/r1)

RADIO DEL CONO

d1-d2= Q/2πT ln (r2/r1)

CALCULAR EL DESCENSO

HIPOTESIS A TENER EN CUENTA

El caudal extraído no puede volver al acuífero.

Alimentación continúa, el caudal extraído mediante bombeo es igual al caudal que ingresa (de alimentación del acuífero).

El medio es homogéneo e isótropo.

La componente vertical de la velocidad es casi nula con relación a la componente horizontal.

La ley de Darcy es aplicable.

Superficies equipotenciales planas. La componente horizontal de la velocidad de todas las líneas de corriente es la misma en todos los puntos de una misma vertical.

El agua y el suelo del acuífero son incompresibles.

Pozo que atraviese el acuífero en todo su espesor, o pozo completo

Régimen permanente

Conociendo los parametros del acuifero podemos

Calcular el radio del cono de descensos

Si a cierta distancia existe en superficie una fuente de contaminación, podremos calcular si el cono de descensos llega hasta el punto contaminante

Calcular el Descenso

Producido por un caudal dado a cierta distancia

Calcular el Caudal

Se obtiene sin superar un cierto descenso

Estudio de distintos modelos matemáticos, que con la aplicacion de ciertas hipotesis se determinan parametros hidrodinámicos