jonka Nicolás Guevara 5 vuotta sitten
2594
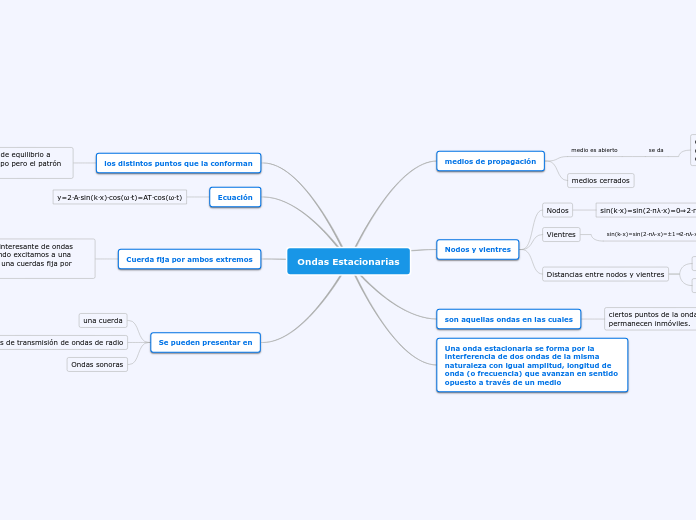
Ondas Estacionarias
jonka Nicolás Guevara 5 vuotta sitten
2594

Lisää tämän kaltaisia
la cuerda es L, y debe cumplirse que en los extremos límites (condiciones de contorno) x=0 y x= L. Tiene que haber un nodo, es decir, una zona de ausencia de vibraciones o de mínima energía y un antinodo o punto donde la energía es máxima
•Instrumentos de cuerda
x2−x1=(2⋅2+1)⋅λ4−(2⋅1+1)⋅λ4=λ2
x2−x1=2⋅λ2−1⋅λ2=λ2
cuando la propagación no encuentra ningún obstáculo que refleje las ondas hacia el foco emisor
en estos
la energía avanza en un único sentido