jonka Erwin Oswaldo Salazar Espinoza 4 vuotta sitten
535
Organigrama arbol
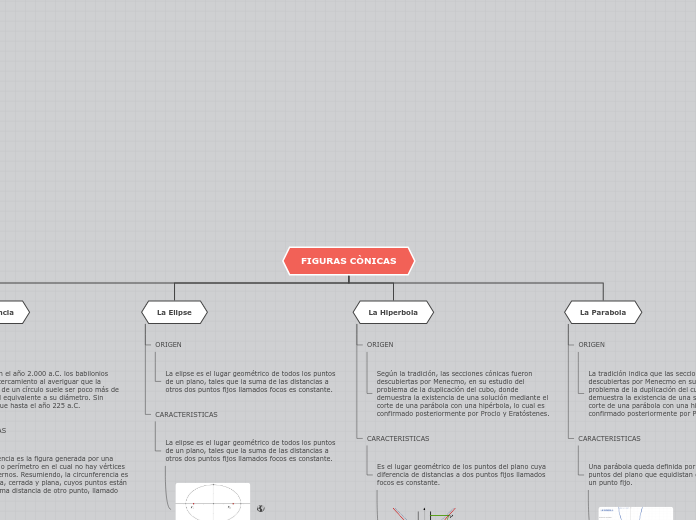
Las secciones cónicas son figuras geométricas estudiadas desde la antigüedad, con importantes contribuciones atribuidas a Menecmo y otros matemáticos clásicos. Entre estas figuras destacan la hipérbola, la circunferencia, la parábola y la elipse, cada una con sus características y orígenes particulares.