jonka Sofia Nogueiras 3 vuotta sitten
269
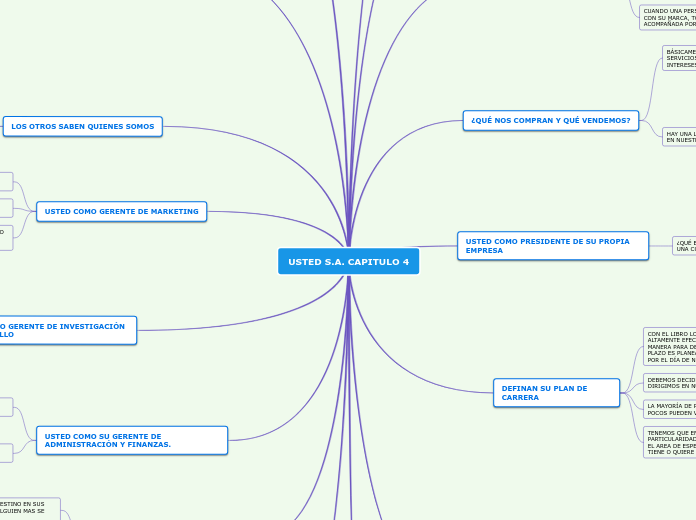
Organigrama arbol
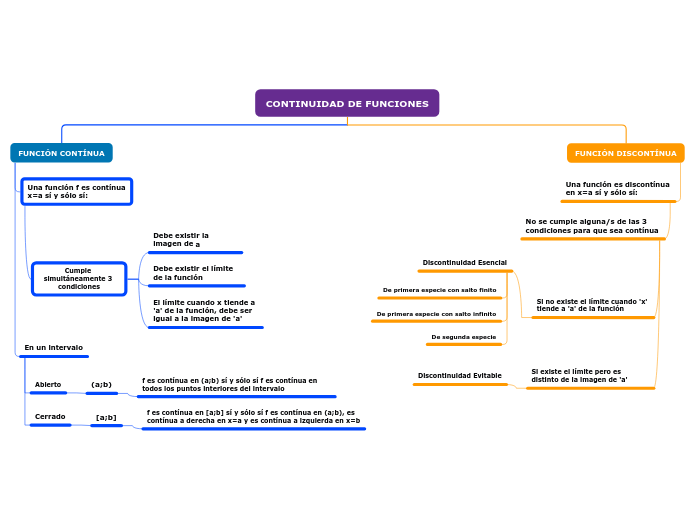
Para determinar la continuidad de una función en un punto específico, deben cumplirse tres condiciones simultáneamente: la función debe estar definida en ese punto, el límite de la función al aproximarse a dicho punto debe existir, y este límite debe ser igual al valor de la función en ese punto.