jonka Maicon Douglas Onofre 2 vuotta sitten
318
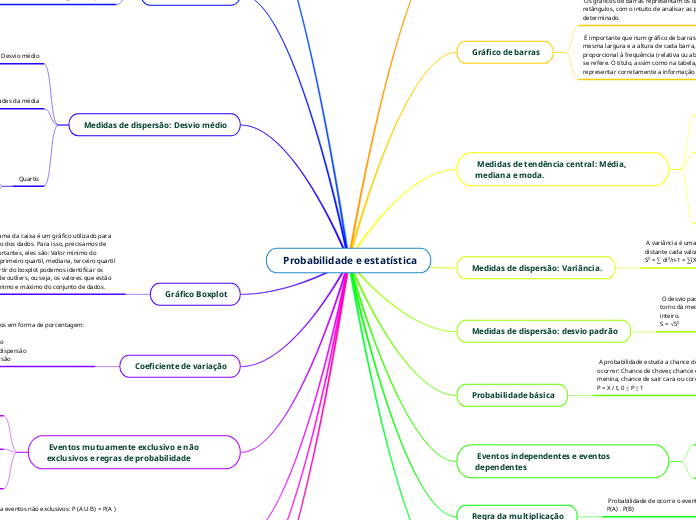
Probabilidade e estatística
jonka Maicon Douglas Onofre 2 vuotta sitten
318

Lisää tämän kaltaisia