jonka Rushikesh Amin 3 vuotta sitten
8692
Quadratics Concept Map Assignment
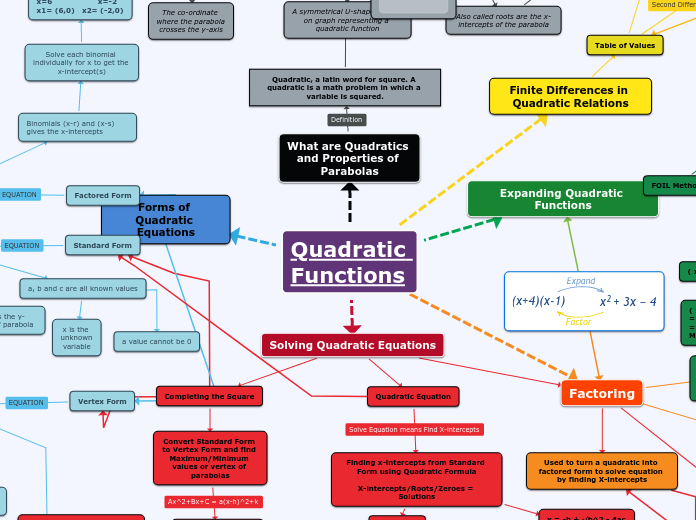
jonka Rushikesh Amin 3 vuotta sitten
8692

Lisää tämän kaltaisia
x^2-5^2 =x^2-25
Ex. a=2 Step Pattern =2[1,3,5,7,9] =2,6,10, 14, 18
If k>0, it is a vertical shift up by k units. If k<0, it is a vertical shift down by k units.
If h>0, it is a horizontal shift to the right. If h<0, it is a horizontal shift to the left
y=0.5(x-6)(x+2) -------------------------- x-6=0 x+2=0 x=6 x=-2 x1= (6,0) x2= (-2,0)
adding x-intercepts and then dividing by 2 = axis of symmetry - midpoint of x-intercepts
(6,0) and (-2,0) ------------------ =[6+(-2)]/2 =[4]/2 =2 Axis of Symmetry is (2,0) X value of vertex is 2 - (2,y)=vertex
axis of symmetry is the x value of the vertex
(b^2-4ac)
Discriminant
Negative discriminant = no real roots
If discriminant is zero there is 1 root
Positive discriminant = 2 roots
x = -b ± √b^2 - 4ac ________________ 2a
2=-3x^2+4x+2
1. Make sure L.S or R.S is equal to 0
0=-3x^2+4x+2
5. Solve for x2
4. Repeat except make the addition sign between -b and square root subtraction
3. Solve for x1
a=-3, b= 4, c= 2 2. Sub in a, b, and c values in formula
y=3x^2-12x-5 y=(3x^2-12x)-5 y=3(x^2-4x)-5 -4/2=-2^2=4 y=3(x^2-4x+4)-5 y=3(x^2-4x+4)-17 y=3(x-2)^2-17
8. Write out the final Equation that is left over
7. Keep the "a" value outside bracket and square root the first term x^2, keep the sign of the middle term (addition or subtraction) and square root the last term in bracket, add a square outside of end bracket to give you: (x-h)^2
5. Move the opposite sign (b/2)^2 value outside bracket by multiplying it by "a" value
6. Add this value with the k value outside bracket to get final k value
4. Add the opposite sign of the (b/2)^2 inside the bracket EX. 2(x^2+6x+9-9)+11
3. Make Perfect Square Trinomial inside bracket using: (b/2)^2
2. Common Factor the "a" value
1. Put brackets around ax^2+bx terms
Vertex = (2,17) Minimum = -17
a^2 - b^2 = (a+b)(a-b)
a^2 = 144p^2 so a = √144p2 = 12p b^2 = 81 so b = √81 = 9
Sub. in a and b into reference equation to get factored
Ax^2+Bx+C =144p^2+0x-81 =144p^2-81 =(12p+9)(12p-9)
Identifying Characteristics
Contains Perfect Squares
Contains a difference (Subtraction)
Contains Binomials (2-terms)
Same method of factoring is used as factoring trinomials except you write the product as the square of a binomial
First and last terms are perfect squares
a^2±2ab+b^2 = (a±b)^2
Check that "2ab" is the middle term
2ab = 2(2x)(3) = 4x(3) = 12x
Therefore, 2ab is the middle term and that means it is a square trinomial
Using this as a reference equation find out what a and b are
a^2 = 4x^2 so a=√4x^2 = 2x b^2 = 9 so b=√9 = 3
4x^2+12x+9 4(9) = 36 m(n)=36 m = 6 n+n=12 n = 6 Sub. in numbers as bx term = 12x =4x^2+6x+6x+9 =2x(2x+3)+3(2x+3) =(2x+3)(2x+3) =(2x+3)^2
6. The last two binomials should be the same and so you simplify them together by writing the product as the square of the binomial
E.g. (2x – 3)(2x – 3) = (2x – 3)^2
5. Group the terms with common factors and factor each binomial group
4. Substitute the two numbers for the middle term
3. Multiply a value and c value -Find two numbers that multiply to the product of a(c) and have the sum of b
2. Move GCF outside of bracket
1. Factor out the GCF by dividing it with all terms
Trinomial Standard Form ax^2+bx+c ---------------------------- 2x^2+10x-12 =2(x^2+5x-6) =2(x^2-1x+6x-6) =2(x(x-1)+ 6(x-1) =2(x-1)(x+6)
x-1=0 x+6=0 x=1 x=-6
If the trinominal cannot be common factored and the a value is more than 1, you have to multiply a and c
m(n)=a(c) m+n=b
4. Factor by grouping
3. Find Two integers that multiply to "c" and add to "b"
m*n=-6 m+n=-5 -1*6=-6 -1+6=5
Sub. in these numbers for b value
These two integers end up being (x-r) and (x-s) in factored form
1. Common Factor (If Any) Common Factor = 2
Binomial Common Factor
2(x+1)-3y(x+1) _____________ (x+1) = (x+1)(2-3y)
Monomial Common Factor
12 x^2y-9x^3y^2z+18x^2y^2 _________________________ 3x^2y =3x^2y(4-3xyz+6y)
Divide each term by the GCF and write what remains in bracket
Move GCF outside of bracket
Identify greatest common factor = 3x^2y
If First Differences are constant, there is a linear relation
Optimal Value
The lowest or highest value/peak or bottom of the parabola depending on the a value - UPWARD or DOWNWARD?
Y-intercept
The co-ordinate where the parabola crosses the y-axis
Axis of Symmetry
Axis of Symmetry is the sum of the roots divided by two
A vertical line that divides the parabola into two equal halves
Zeroes
Also called roots are the x-intercepts of the parabola
Can have one, two or zero roots
A symmetrical U-shaped curve on graph representing a quadratic function