jonka De carvalho gauthier 3 vuotta sitten
298
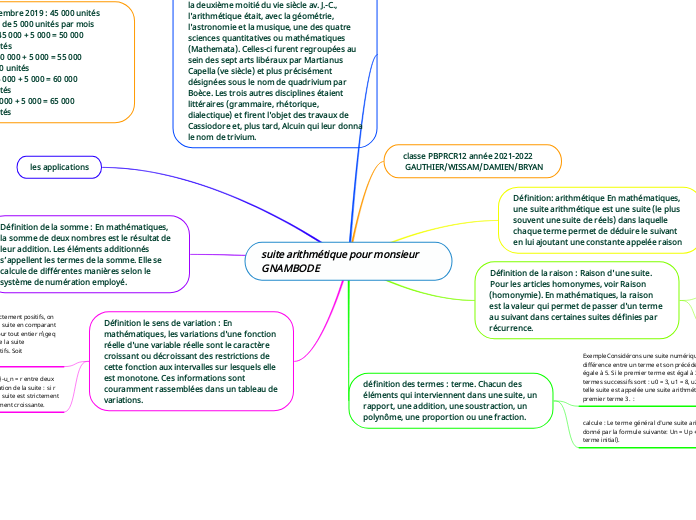
suite arithmétique pour monsieur GNAMBODE
jonka De carvalho gauthier 3 vuotta sitten
298

Lisää tämän kaltaisia