DERIVACIÓN
Derivación compuesta
La derivada compuesta es una regla para encontrar la derivada de una función compuesta.
Si tenemos una función compuesta f(x) = g(h(x)), entonces la derivada compuesta se denota como f'(x) = g'(h(x)) * h'(x)
SE APLICA A
Funciones Trigonometricas Compuestas
Para y = cos(3x)
d/dx cos(3x) = -sen(3x) * 3 = -3 sen(3x)
Funciones Exponenciales
Para y=e^5x
d/dx e^5x = e^5x * 5 = 5e^5x
Funciones Potenciales Compuestas
Para y = (2x + 3)^4
d/dx (2x + 3)^4 = 4(2x+3)^3 * 2 = 8(2x+3)^3
Funciones Logarítmicas
Para y = Ln(4x)
d/dx ln(4x) = 1/4x * 4 = 1/x
La derivada compuesta cuenta
con una regla que nos indica de
cómo hallar la derivada de F = gof.
Derivación de orden superior
Sea f una función

Figueroa (2000
MITACC & TORO (2009)
Derivación implicita
Técnica utilizada para encontrar la derivada de una función que no está expresada de forma explícita en términos de una sola variable.
Aplicación: Se utiliza cuando una ecuación relaciona varias variables y no se puede despejar una de ellas de manera explícita.
Proceso:
1. Se deriva la ecuación con respecto a la variable independiente.
2. Se identifican las derivadas de las variables dependientes e independientes.
3. Se despeja la derivada deseada de la ecuación resultante.
Ejemplo:
x^2+y^2=25
d/dx(x^2) + d/dx (y^2)=d/dx (25)
2x+2ydy/dx=0
dy/dx = -x/y
Aplicaciones Prácticas:
-Geometría Analítica
-Física
-Economía
Las derivadas de orden superior no afectan directamente la recta tangente pero proporcionan informacion
f'(x)
Determina la pendiente en un punto
especifico
f''(x)
Indica la concavidad de la curva
f′′(x) > 0
La curva es concava
hacia arriba en ese punto
f′′(x) < 0
La curva es concava
hacia abajo en ese punto
Se obtiene derivando ambas partes de la ecuacion implicita con respecto a “x” y luego resolviendo para dy/dx
REGLA DE LA CADENA
Importancia
Fundamental en la derivación compuesta.
Enunciado
Si g es derivable en x y f es derivable en (gx),
la función compuesta F = f o g definida mediante
F(x) = f(g(x)) es derivable en x.
Fórmula
La derivada de F en x es igual a la derivada de f en g(x) multiplicada por la derivada de g en x
Denotado matematicamente por:
f'(x) = f'(g(x)).g'(x)
Sirve para derivar
Potencias y raíces de funciones
Funciones trigonometricas
Funciones exponenciales y logaritmicas
Derivación implicita
Pendiente
Thomas & Weir (2016)
Anton, Bivens & Davis (2010)
Formula de Leibniz
RECTA NORMAL
en
en
en
y
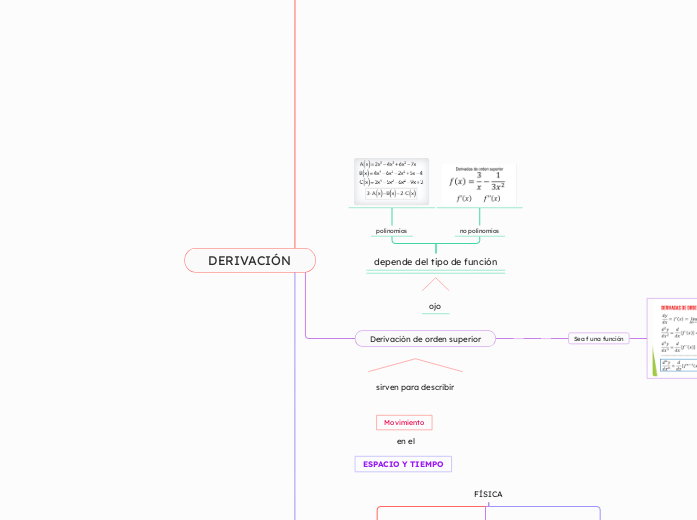
depende del tipo de función
polinomios
no polinomios

Movimiento
en el
ESPACIO Y TIEMPO
sirven para describir
TANGENTE
ECUACION DE LA PENDIENTE
Derivación compuesta
Steward (2020)
James (2012)
Derivación de orden superior
Simmons (1991)
Zill y Wright (2013)
Derivación implicita
Larson y Edwards (2009)
ECUACION DE LA RECTA TANGENTE
Derivación compuesta
James (2012)
Derivación implicita
Larson y Edwards (2009)
ojo

Negativo reciproco de la pendiente
de la recta tangente
Ecuacion de la Recta Normal
Thomas & Weir (2016)
Anton, Bivens & Davis (2010)
La recta
normal es perpendicular a la recta tangente en un punto dado de la curva
FÍSICA