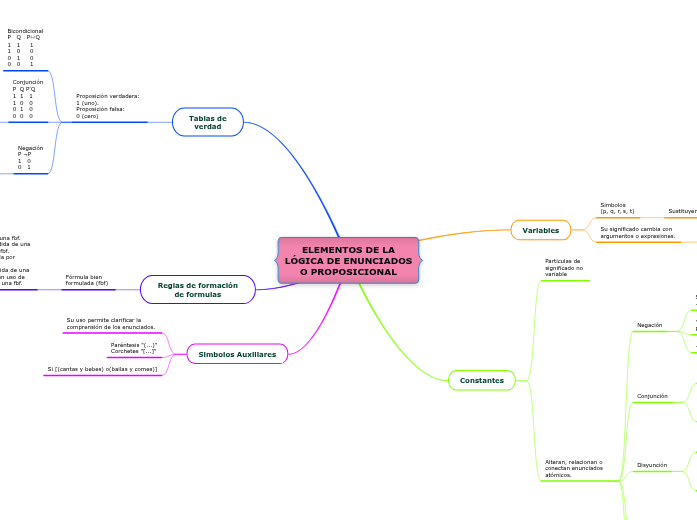
ELEMENTOS DE LA LÓGICA DE ENUNCIADOS O PROPOSICIONAL

Simbolos (p, q, r, s, t)

Sustituyen proposiciones o enunciados.

Su significado cambia con argumentos o expresiones.

Ejemplo:
p= La Tierra es un planeta.

Particulas de significado no variable

Alteran, relacionan o conectan enunciados atómicos.

Negación

Se simboliza con: ¬. (También: - , ~)

Representa la partícula lingüística "no" u otras con la idea de negación.

"No es el caso que, no pasa que, ni, etc."

¬p, ¬q, ¬r, ¬s, t¬.

¬p: La luna no tiene satélites. p: La luna tiene satélites.

Conjunción

Se simboliza con: ˄ (También: ·, & ) = y

Representa la partícula lingüística "y"

Indica la idea de unión (también, igualmente, pero).

p: Marte tiene satelites.
q: Jupiter tiene satélites.
p ˄ q
"Marte tiene satélites y Júpiter también".

Disyunción

Se simboliza con: ˅= (o)

Representa la partícula lingüística "o"

Tiene dos sentidos: uno inclusivo y otro exclusivo.

p: Se aprende lógica escuchando la clase.
q: Se aprende lógica estudiando
p ˅ q
"Se aprende lógica escuchando la clase o estudiando"

Condicional

Se simboliza con: → (También: ⊃ )

Representa las partículas lingüísticas si p entonces..q

"cuando...entonces..., entonces o una simple "coma" (,)

"entonces" o "equivalente" separa el antecedente del consecuente.

p: Llueve q: La tierra se moja. p → q
"Si llueve, entonces la tierra se moja".

Bicondicional

Se simboliza con: ↔ (También:≡ )

Representa las partículas lingüísticas si y sólo si…

Indica doble condición, equivale, cuando y solo cuando

Condición necesaria y suficiente

p: Es de noche. q: Se ha ocultado el Sol. p ↔ q
"Es de noche si y sólo si se ha ocultado el sol".

Proposición verdadera: 1 (uno).
Proposición falsa: 0 (cero)

Bicondicional
P Q P⇔Q
1 1 1
1 0 0
0 1 0
0 0 1

Conjunción
P Q P˄Q
1 1 1
1 0 0
0 1 0
0 0 0

Condicional
P Q P⇒Q
1 1 1
1 0 0
0 1 1
0 0 1

Negación
P ¬P
1 0
0 1

Disyunción
P Q P˅Q
1 1 1
1 0 1
0 1 1
0 0 0

Fórmula bien formulada (fbf)

1. Una variable proposicional es una fbf.
2. Una fbf precedida de una negación es una fbf.
3. Una fbf seguida por cualquiera de las constantes, seguida de una fbf, haciendo buen uso de los paréntesis es una fbf.

Su uso permite clarificar la comprensión de los enunciados.

Paréntesis "(...)"
Corchetes "[...]"

Si [(cantas y bebes) o(bailas y comes)]