Geometry/Measurement Project
Geometric Figures
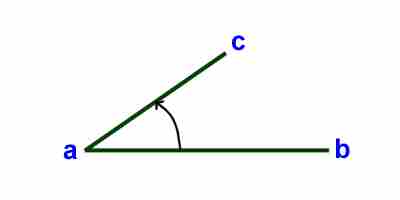
Angle- The point when two line segments meet
together
Corresponding Angles- Two angle sums that add up to 90°
Supplementary Angles- Two angle sums that add up to 180°
Congruent Angles- These are two angles that have the same measure
Angle Measure- the number of degrees of turn to rotate about the vertex
Corresponding Angles- When two lines are crossed by another line, the angles in matching corners are called corresponding angles.
Classification of Angles-
Right Angle- two line segments that have an angle of 90°
Obtuse Angle- Two line segments that have an angle greater than 90°
Acute Angle- Two line segments that have an angle less then 90°
Straight Angle- a line segment that equals 180°
Sum Of Angles For A Triangle- All three angles should add up to 180°.
Types of Polygons, Triangles, Quadrilateral, and Circles
Polygon- Is a simple closed polygonal curve.

A triangle has 3 sides
Quadrilateral has 4 sides


Pentagon has 5 sides
Triangle
Acute Triangle- all three interior angles are acute (the angles have to be less than 90°)
Right Triangle- if one angle is a right angle ( the angle equals 90°)
Obtuse Triangle-If an interior angle is obtuse (if the angle is greater than 90°)
Scalene- No two sides of the triangle have the same length
Isosceles- At least two sides of the triangle have the same length sides
Equilateral- All three sides have to be the same length
Quadrilaterals is any shape that has 4 sides
A kite has two pairs of adjacent congruent sides
A trapezoid has two parallel sides
Isosceles Trapezoid has two sides parallel and two congruent angles
A parallelogram has two pairs of opposite parallel sides
A rhombus is a parallelogram with all the sides of the same length.
A rectangle is a parallelogram with all right angles.
A square has all the sides are the same length and all right angles.
Circle- This shape is different because it does not have any sides.
A regulare polygon is a convex polygon that is both equilateral and equiangular

Alternative Interior Angles- (<f and <d) also (<e and <c )
Alternate Exterior Angles- (<b and <h) also (<a and <g)
Corresponding Angles- (<b and <f) also (<a and <e) also (<d and <h) also (<c and <g)
Volume
The volume of a figure is the number of cubes required to fill it completely. Volume is measured in "cubic" units. An easy way to understand and remember volume is by listening to the volume song for kids: http://www.youtube.com/watch?v=JijhDDJvExo


Volume of a pyramid

Volume of a cone

Volume of a prism
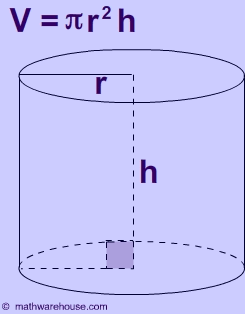
Volume of a cylinder
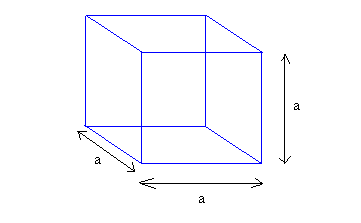
Volume of a cube
Polyhedron: a three-dimensional figure made up of sides called faces, each face being a polygon
To determine the volume of a polyhedron, follow the steps below:
1. center the polyhedron at the orgin of the 3-dimensional rectangular coordinate system
2. draw lines from each vertex (corner) to the orgin. Each face is now the base of a pyramid with the orgin as its apex.
3. Calculate the volume of each pyramid. Using pyramids volume formula ( V=(1/3)B*h where B is the area of the base.
4. Add together the volumes of all the pyramids to get the entire volume of the polyhedron.
Perimeter
Perimeter is the distance around a plane figure where you add up all of the sides.

Circumference is the name of the perimeter of a circle. The equation is C= 2*pi*r where r is the radius. This also means that C=2pi*r
Prisms
A prism has 2 congruent faces (the bases) in parallel planes and other faces (lateral faces) bounded by parallelograms
Subtopic
If you are looking at a 2 dimensional figure you can still visulize a prism and define the characteristics.
-you can determine this by the amount of sides and name them from that amount of sides. For example the picture below you can see the bases are triangles and the sides are rectangles even tho the picture is only 2 dimensional.

The right prism has two lateral faces that are perpendicular to the bases.
An oblique prism has lateral faces that are NOT perpendicular to the faces.
You can easily tell the shape of a prism by its name. For example a triangle right prism has 2 triangle bases meaning there are three sides that have a right angle. A hexagonal oblique prism will be tilted and not have any right angles at all because it is hexagonal we know that it has 6 sides.
Surface Area
Surface area is the sum of the lateral surface areas and the area of the bases
Equations
Cube
6(eXe)
, for a cube with side lengths of 5, you would solve it like so 6(5X5), 6(25), The surface area is 150 Units^2undefined
Prism
PH+2B
This equation takes a lot of explaining, for example P=the perimeter of the base, H=the height of the prism, and B=the AREA of the base
An example would be, P=12, H=10, and B=6. The equation would then be (12X10)+(6X2)- resulting in an answer of 132Units^2undefined
Cylinder
PH+2B
This equation is similar to the prism, only the area of the base would be circular, therefore the "2b" become "2piR^2" and the "PH" becomes "2piRXH"
A cylinder with Radius 2 and Height 4 would be, 2pi(2^2)+ 2pi2X4, 8pi+16pi, or 24pi (Units^2)
Pyramid
B+1/2ps
In this equation B=the area of the base, p=number of sides and s=slant height
For example a pyramid with four sides, a slant height of 3, and a base area of 12 would be, 12+1/2(3X4), 12+6, 18Units^2undefined
Cone
piR^2+piRXs
In this equation S=slant height and R=Radius of the base
A cone with a slant height of 4, and a radius of 6 would be pi6^2+pi6X4, 36pi+24pi=60piUnits^2undefined
Sphere
4piR^2
When radius =3, 4pi(3^2), 4pi(9), 36piUnits^2undefined
You can always just add up the area of all the sides, but there are some equations and tricks to avoiding the hassle and uncertainty of that!
Pythagorean Theorem
The equation for the Pythagorean Theorem is a^2+b^2=c^2undefined
It is important to remember "C" is always the hypotenuse of the triangle

Subtopic
In this example lets say A=3 B=4 and C is unknown
You would solve "C" by using the equation, 3^2+4^2=C^2, you would then get 9+16=C^2, 25=C^2, C=5 units
The pythagorean theorem only works for right triangles, therefore you can determine if triangle is right by plugging the numbers into the equation
Lets say A=2 B=5 and C=10
2^2+5^2 = 10^2, 4+25=100, or 29=100. This is incorrect, therefore you have identified that this triangle is not a right triangle.
Area
Area is the surface size of a figure. Area is always expressed in units squared.

The area of a circle

Area of a rectangle: length times width
Area of a parallelogram: base times height
Area of a triangle: 1/2 times base times height
Area of a trapezoid: 1/2 (base A + base B) times H
