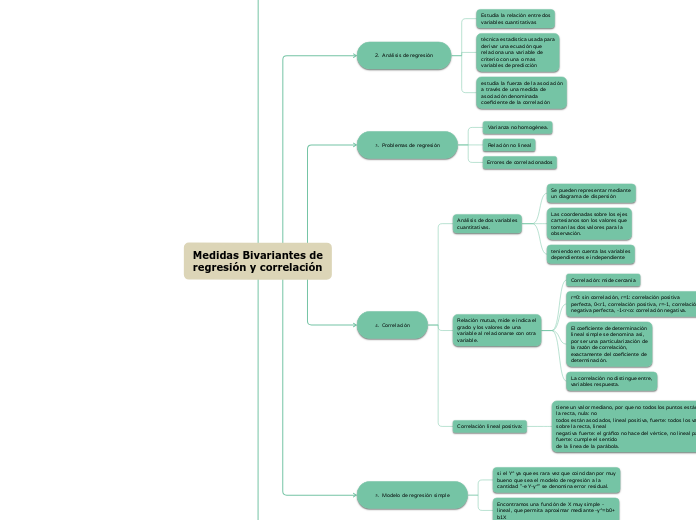
Medidas Bivariantes de
regresión y correlación

coeficiente de determinación R2

Correlación lineal simple.

correlación positiva y correlación negativa

Diagramas de dispersión

Regresión

Regresión simple

Estudia la relación entre dos
variables cuantitativas

técnica estadística usada para
derivar una ecuación que
relaciona una variable de
criterio con una o mas
variables de predicción

estudia la fuerza de la asociación
a través de una medida de
asociación denominada
coeficiente de la correlación

Varianza no homogénea.

Relación no lineal

Errores de correlacionados

Análisis de dos variables
cuantitativas.

Se pueden representar mediante
un diagrama de dispersión

Las coordenadas sobre los ejes
cartesianos son los valores que
toman las dos valores para la
observación.

teniendo en cuenta las variables
dependientes e independiente

Relación mutua, mide e indica el
grado y los valores de una
variable al relacionarse con otra
variable.

Correlación: mide cercanía

r=0: sin correlación, r=1: correlación positiva
perfecta, 0<r1, correlación positiva, r=-1, correlación
negativa perfecta, -1<r<o: correlación negativa.

El coeficiente de determinación
lineal simple se denomina así,
por ser una particularización de
la razón de correlación,
exactamente del coeficiente de
determinación.

La correlación no distingue entre,
variables respuesta.

Correlación lineal positiva:

tiene un valor mediano, por que no todos los puntos están incluidos en la recta, nula: no
todos están asociados, lineal positiva, fuerte: todos los valores están sobre la recta, lineal
negativa fuerte: el gráfico no hace del vértice, no lineal parabólica fuerte: cumple el sentido
de la linea de la parábola.

si el Y^ ya que es rara vez que coincidan por muy
bueno que sea el modelo de regresión a la
cantidad "-e Y-y^" se denomina error residual.

Encontramos una función de X muy simple -
lineal, que permita aproximar mediante -y^=b0+
b1X

Coeficiente de correlación lineal
de Pearson.

Si los puntos tienen una tendencia a
disponerse alineadamente

R es útil para determinar si hay
relación lineal entre dos
variables, pero no servirá para
(cuadráticas, logarítmica)

tiene un mismo signo que
S(X,Y)