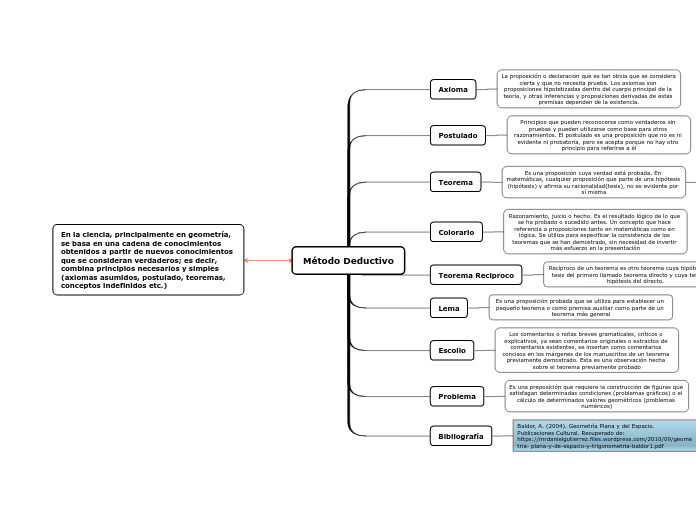
Método Deductivo

Axioma

La proposición o declaración que es tan obvia que se considera cierta y que no necesita prueba. Los axiomas son proposiciones hipotetizadas dentro del cuerpo principal de la teoría, y otras inferencias y proposiciones derivadas de estas premisas dependen de la existencia.

Postulado

Principios que pueden reconocerse como verdaderos sin pruebas y pueden utilizarse como base para otros razonamientos. El postulado es una proposición que no es ni evidente ni probatoria, pero se acepta porque no hay otro principio para referirse a él

Teorema

Es una proposición cuya verdad está probada. En matemáticas, cualquier proposición que parte de una hipótesis (hipótesis) y afirma su racionalidad(tesis), no es evidente por sí misma

Consta de dos
partes principales

Lo que se supone

Lo que se quiere demostrar

Colorario

Razonamiento, juicio o hecho. Es el resultado lógico de lo que se ha probado o sucedido antes. Un concepto que hace referencia a proposiciones tanto en matemáticas como en lógica. Se utiliza para especificar la consistencia de los teoremas que se han demostrado, sin necesidad de invertir más esfuerzo en la presentación

Teorema Reciproco

Recíproco de un teorema es otro teorema cuya hipótesis es la tesis del primero llamado teorema directo y cuya tesis es la hipótesis del directo.

Lema

Es una proposición probada que se utiliza para establecer un pequeño teorema o como premisa auxiliar como parte de un teorema más general

Escolio

Los comentarios o notas breves gramaticales, críticos o explicativos, ya sean comentarios originales o extractos de comentarios existentes, se insertan como comentarios concisos en los márgenes de los manuscritos de un teorema previamente demostrado. Esta es una observación hecha sobre el teorema previamente probado

Problema

Es una preposición que requiere la construcción de figuras que satisfagan determinadas condiciones (problemas gráficos) o el cálculo de determinados valores geométricos (problemas numéricos)

Bibliografía

En la ciencia, principalmente en geometría, se basa en una cadena de conocimientos obtenidos a partir de nuevos conocimientos que se consideran verdaderos; es decir, combina principios necesarios y simples (axiomas asumidos, postulado, teoremas, conceptos indefinidos etc.)