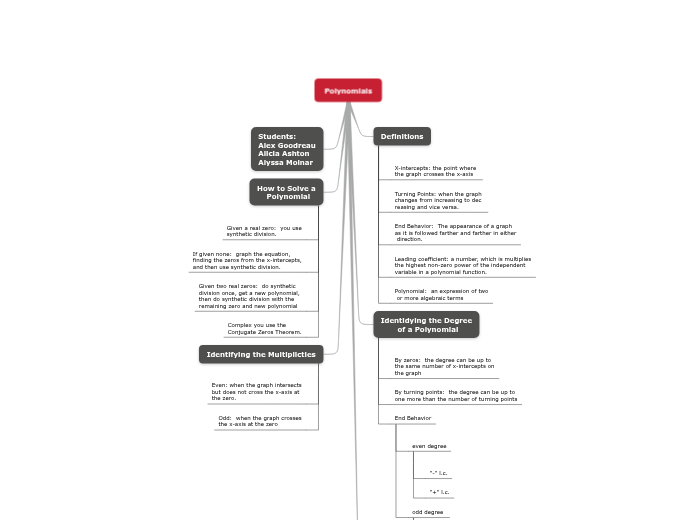
Polynomials
Definitions
X-intercepts: the point where
the graph crosses the x-axis
Turning Points: when the graph
changes from increasing to dec
reasing and vice versa.
End Behavior: The appearance of a graph
as it is followed farther and farther in either
direction.
Leading coefficient: a number, which is multiplies
the highest non-zero power of the independent
variable in a polynomial function.
Polynomial: an expression of two
or more algebraic terms
Identidying the Degree
of a Polynomial
By zeros: the degree can be up to
the same number of x-intercepts on
the graph
By turning points: the degree can be up to
one more than the number of turning points
End Behavior
even degree
"-" l.c.
"+" l.c.
odd degree
"+" l.c.
"-" l.c.
Identifying of Number
of Zeros
Real: a polynomial of degree n
has at most n distinct zeros
Complex: a polynomial f(x) of degree n, with n is
greater than or equal to one, has at least one
complex zero
Students:
Alex Goodreau
Alicia Ashton
Alyssa Molnar
How to Solve a
Polynomial
Given a real zero: you use
synthetic division.
If given none: graph the equation,
finding the zeros from the x-intercepts,
and then use synthetic division.
Given two real zeros: do synthetic
division once, get a new polynomial,
then do synthetic division with the
remaining zero and new polynomial
Complex you use the
Conjugate Zeros Theorem.
Identifying the Multiplicties
Even: when the graph intersects
but does not cross the x-axis at
the zero.
Odd: when the graph crosses
the x-axis at the zero