RAZONES Y PROPORCIONES
REGLA DE TRES
Método utilizado para resolver problemas de proporcionalidad directa e inversa
EJEMPLOS
TALLER

PORCENTAJES
Un porcentaje indica la parte que se toma de una cantidad por cada cien unidades. Su cálculo corresponde a un problema de proporcionalidad directa.
TALLER
TALLER 2
PROPORCIONALIDAD
DEFINICIÓN
Magnitud es toda propiedad de las cantidades que se puede medir. Son magnitudes: el tiempo, la velocidad, la distancia, el peso, la superficie, el volumen, entre otras.
La relación entre las diferentes magnitudes puede ser directa o inversamente proporcional.
TIPOS
Magnitudes directamente proporcionales
Dos magnitudes x y y, son directamente proporcionales cuando están relacionadas por una función de la forma y = k . x, siendo k una constante distinta de cero, denominada factor o coeficiente de proporcionalidad.
Dos magnitudes son directamente proporcionales cuando al aumentar una de ellas, la otra también aumenta en la misma proporción, si una disminuye la otra también disminuye en la
misma proporción.
Magnitudes inversamente proporcionales
Dos magnitudes x y y, son inversamente proporcionales cuando se tiene una relación de la forma y=k/x , siendo k una constante distinta de cero, denominada factor o coeficiente de proporcionalidad.
Es decir, dos magnitudes son inversamente proporcionales cuando al aumentar una de ellas, la otra disminuye en la misma proporción y viceversa
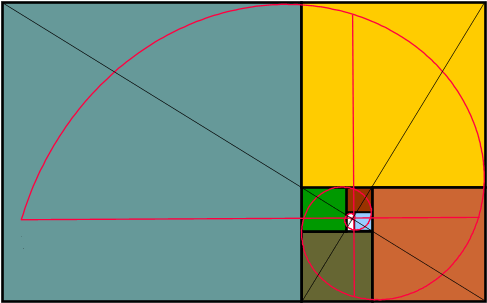
RAZÓN ÁUREA
DEFINICIÓN
Durante los últimos siglos, creció el mito de que los antiguos griegos estaban sujetos a una proporción numérica específica, esencial para sus ideales de belleza y geometría: Dicha proporción es conocida con el nombre de proporción áurea o divina proporción. Aunque recientes investigaciones revelan que no hay ninguna prueba que conecte esta proporción con la estética, sigue manteniendo cierto atractivo de belleza.
La razón áurea se simboliza con la letra griega (fi), el valor numérico es aproximadamente 1,61 está dado por el cociente (1+raíz cuadrada de 5)/2
EJEMPLOS
La razón áurea también se puede encontrar en otras figuras geométricas, por ejemplo el pentágono regular, en el que la razón entre la diagonal y el lado cumple la divina proporción.
Hay enigmáticas conexiones de la espiral de los nautilius (un tipo de caracola) y las espirales de los girasoles con la razón áurea.
Este OA incluye los temas fundamentales sobre razones y proporciones, la definición, las propiedades y algunas aplicaciones.
OBJETIVO DEL OA
Brindarle al estudiante las herramientas necesarias para resolver problemas que involucren situaciones cotidianas de la empresa en las que pueda demostrar un buen manejo del concepto y de las aplicaciones de porcentajes, razones y proporciones.
RESULTADOS DE APRENDIZAJE
Tipo Cognoscitivo
· Comprende y aplica el concepto de proporcionalidad
· Identifica las propiedades de las razones y proporciones
· Analiza el concepto de proporcionalidad y su aplicación en situaciones o problemas que describen variaciones y cambios de diferentes variables.
Tipo Socio-Afectivo
· Aumenta la capacidad y potencial matemático para comprender, interpretar, analizar y solucionar situaciones problémicas que requieren de la proporcionalidad.
· Adquiere capacidad para trabajar grupalmente, aportar y analizar diferentes opciones en la solución de situaciones problémicas y ejercicios complementarios.
Tipo Profesional
Aplica conceptos y procesos operativos propios de las razones y proporciones en la solución de algunos problemas propios de la ingeniería y otras profesiones.
Facilita patrones matemáticos para modelar y resolver problemas de proporcionalidad
INFORMACIÓN AUTORA
Luz Mary Ariza N.
Licenciada en Matemáticas. luzariza@unipanamericana.edu.co.
Profesora Institución Universitaria Unipanamericana
REFERENCIAS Y ENLACES
http://revistasuma.es/IMG/pdf/44/065-070.pdf
http://www.aulafacil.com/matematicas-porcentajes/curso/Lecc-7.htm
http://www.eet6sannicolas.edu.ar/biblioteca/alumnos/noveno/Capitulo%20[1]9mate.pdf
http://www.rena.edu.ve/TerceraEtapa/Matematica/TEMA16/Proporciones.html
http://razonproporcionregladetres.blogspot.com/2009_11_01_archive.html
http://www.inacap.cl/data/sede_virtual/Ayudantias/matematicas_muestra/1_122.asp
http://aritmeticatotal.blogspot.com/2012/01/razones-y-proporciones.html
http://www.edukativos.com/preparatoria/downloads-file-12-details.html
LICENCIA DE USO
(CC-BY-NC-SA)
Reconocimiento al autor
No ccomercializar
Compartir bajo las mismas condiciones
Se aclara que las imágenes no son de autoría propia.
EVIDENCIAS DE APRENDIZAJE
Socialización de las diferentes temáticas y de dudas
Entrega de los talleres según indicación del docente
DEFINICIÓN
RAZÓN
La comparación por cociente entre dos cantidades se denomina razón.
Si a y b son dos cantidades cualesquiera, la razón entre a y b es: a/b se lee "a es a b". También suele escribirse como a:b
PROPORCIÓN
La igualdad entre dos razones se denomina proporción
PROPIEDADES DE LAS PROPORCIONES
Alternar Extremos
Alternar Medios
Permutar
Invertir
Componer respecto al Antecedente y Consecuente respectivamente
Descomponer respecto al Antecedente y Consecuente respectivamente
Componer y descomponer a la vez
Serie de Razones
