INTEGRALES

Áreas

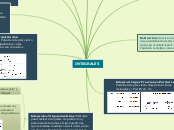
Funciones negativas: Sea una función que f(x)≤ 0. En este caso, la integral definida nos proporciona el área pero, al estar la región por debajo del eje de las abscisas, la integral proporciona un valor negativo.

Funciones negativas: Sea una función que f(x)≤ 0. En este caso, la integral definida nos proporciona el área pero, al estar l

Funciones positivas: Sea una función que f(x) ≥ 0, entonces la integral definida representa el área encerrada entre la gráfica de y el eje de abscisas entre las rectas x=a y x=b

Funciones positivas: Sea una función que f(x) ≥ 0, entonces la integral definida representa el área encerrada entre la gráfic

Entre dos funciones: Ahora tenemos dos funciones f y g, y se desea calcular el área de la región encerrada entre ambas gráficas en el intervalo [a,b]

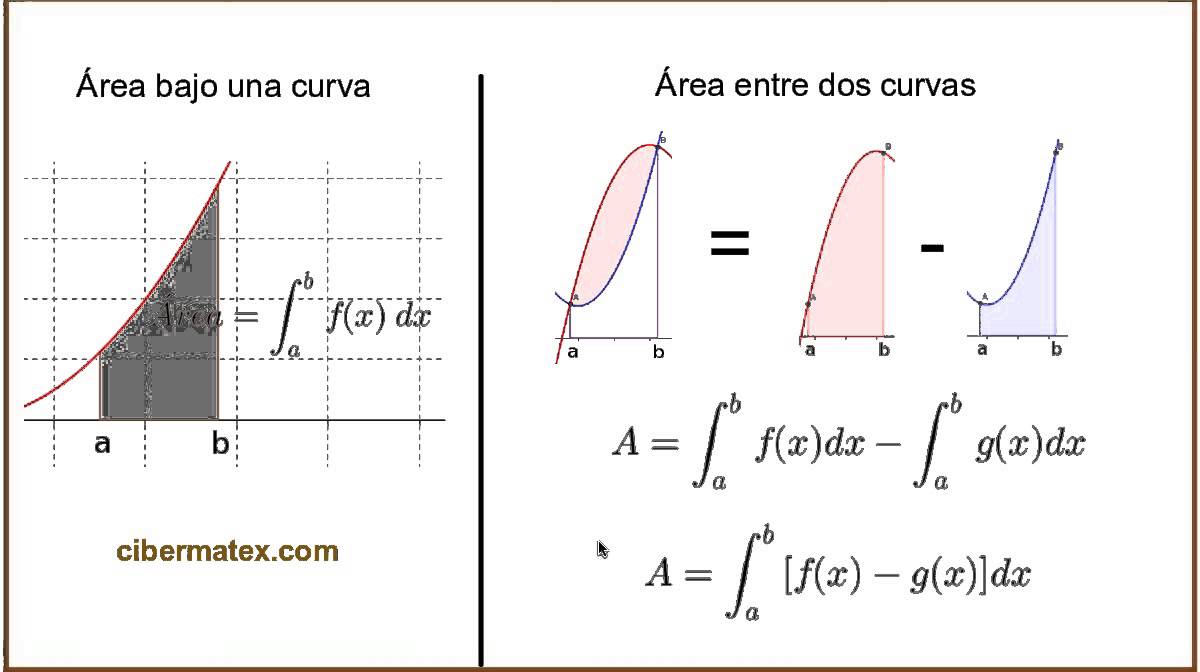
Entre dos funciones: Ahora tenemos dos funciones f y g, y se desea calcular el área de la región encerrada entre ambas gráfic

Integral Indefinida: Es el conjunto de infinitas primitivas que puede tener una fracción

Integral Definida: Sea f(x) continua en a ≤ x ≤ b, la integral definida de f(x) en el intervalo a ≤ x ≤ b es el límite de la suma de Riemann.

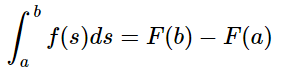
Integral Definida: Sea f(x) continua en a ≤ x ≤ b, la integral definida de f(x) en el intervalo a ≤ x ≤ b es el límite de la
a

Problema de Valor Inicial: Está conformado por una ecuación diferencial ordinaria de primer orden y una condición inicial

Problema de Variaciones: Si Q´(t) es continua en [a,b], entonces la variación total de Q(x) cuando x varía de a hasta b

Problema de Valor Promedio de una Función: Sea f(x) continua en un intervalo [a,b], entonces el valor promedio V de f(x) en [a,b]

Problema de Valor Promedio de una Función: Sea f(x) continua en un intervalo [a,b], entonces el valor promedio V de f(x) en [

Definición: Se dice una función F(x) es una antiderivada de f(x) si F´(x) = f(x) para cada x en el dominio de f.
También se define como el área bajo la curva.

Integración por Fracciones Parciales: Permite integrar cierta clase de funciones racionales ∫ (P(x)/Q(x)) dx

Integración por Fracciones Parciales: Permite integrar cierta clase de funciones racionales ∫ (P(x)/Q(x)) dx

Caso 1: Cuando la factorización de Q(x) se da en factores lineales y distintos

Caso 2: Cuando la factorización de Q(x) es en factores lineales, no necesariamente diferentes

Caso 3: Cuando la factorización de Q(x) produce factores cuadrátricos

Ejemplo:

Ejemplo:

Integración Simple: Son aquéllas que podemos obtener a partir del teorema fundamental del cálculo

Integración Simple: Son aquéllas que podemos obtener a partir del teorema fundamental del cálculo

Integración por sustitución: También se le llama cambio de variable y se basa en la derivada de la función compuesta. Para cambiar de variable, se identifica una parte de lo que se desea integrar con una nueva variable (m), obteniendo así una integral más sencilla

Integración por sustitución: También se le llama cambio de variable y se basa en la derivada de la función compuesta. Para ca

Integración por partes: Permite deducir la fórmula de integración por partes a partir de la regla para derivar un producto de dos funciones. Para recordarla "Un día vi una vaca sin cola vestida de uniforme"

Integración por partes: Permite deducir la fórmula de integración por partes a partir de la regla para derivar un producto de

Integración por sustitución trigonométrica: Permite integrar cierto
tipo de funciones algebraicas cuyas integrales indefinidas son funciones trigonométricas

Integración por sustitución trigonométrica: Permite integrar cierto tipo de funciones algebraicas cuyas integrales indefinida

Caso 1: ax^2 + b donde x = b/a*Tan∝ y dx = b/a*Sec∝ dx

Caso 2: ax^2 - b donde x = b/a*Sec∝*Tan∝ y dx = b/a*Sec∝*Tan∝ dx

Caso 3: b^2-ax^2 donde x = b/a*Sin∝ y dx = b/a*Cos∝

Integrales Trigonométricas: Métodos para resolver integrales de productos y potencias de funciones trigonométricas, que se realizan mediante sustitución junto con algunas identidades trigonométricas.

Caso 1: Potencia de senos y cosenos ∫sinn y ∫cosn donde n es entero positivo impar

Para el Sin, se aplica: Sinnx dx = (sin(n-1)x) (sinx dx) = (1-cos2x)(n-1)/2 (senx dx)

Para el Cos, se aplica: Cosnx dx = (cos(n-1)x) (cosx dx) = (1-sin2x)(n-1)/2 (cosx dx)

Caso 2: Producto de potencias de senos y cosenos ∫sinnxcosmx dx, donde al menos uno de los exponentes entero positivo es par

Caso 2: Producto de potencias de senos y cosenos ∫sinnxcosmx dx, donde al menos uno de los exponentes entero positivo es par

Si n es impar, entonces se aplica: (1-cos2x)(n-1)/2 sinxcosmx dx

Si m es impar, entonces se aplica: (1-sin2x)(n-1)/2sinnxcosx dx

Caso 3: Potencia de senos y cosenos; y producto de potencias de senos y cosenos, donde m y n son enteros positivos pares

Caso 3: Potencia de senos y cosenos; y producto de potencias de senos y cosenos, donde m y n son enteros positivos pares

Para ∫sinnx dx, se aplica = ((1-cos2x)/2)(n/2)

Para ∫cosnxdx, se aplica = ((1+cos2x)/2)(n/2)

Para ∫sinnx dxcosmx dx, se aplica = ((1-cos2x)/2)(n/2)*((1+cos2x)/2)(n/2)

Se representa como ∫ f(x) dx = F(x) + C

Ejemplo: La población P(t) de un suburbio de una gran ciudad en un instante cualquiera, se rige por dP/dt = P[(10)^(-1)-(10)^(-7)] en donde t se mide en meses. ¿Cuál es el valor límite de la población?
¿En qué momento será la población igual a la mitad de su valor límite?

Ejemplo: Una sustancia química fluye en un tanque a razón de 180 + 3t Lt/hrs, donde 0 ≤ t ≤ 10. Encontrar la cantidad de la sustancia química que fluye en el tanque durante la primera hora y durante la segunda hora.

Ejemplo: La altura H(t) de una palmera está dada por H(t) = (t+1)^(1/2) + 5t^(1/3) para 0 ≤ t ≤ 8. Determinar la altura de la palmera si t = 0.48 y determinar el promedio de la altura si 0 ≤ t ≤ 8