SUCESIONES Y SERIES
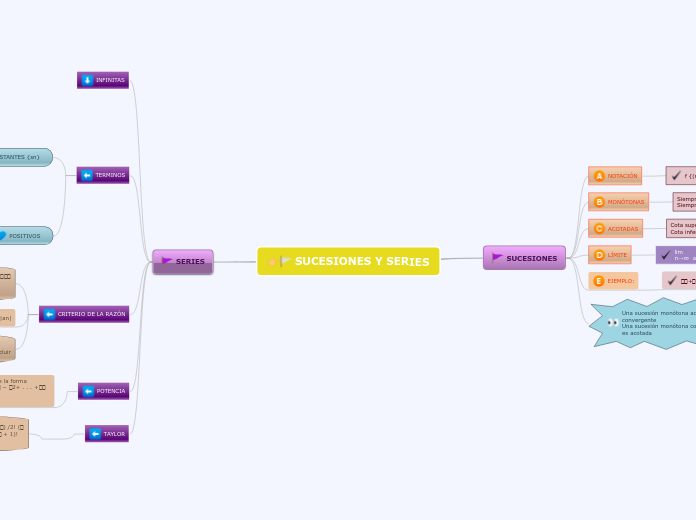
SUCESIONES
NOTACIÓN
f {(n) }, {an} donde f (n) = an
MONÓTONAS
Siempre crecen
Siempre decrecen
ACOTADAS
Cota superior
Cota inferior
LÍMITE
lim
n→∞ an=L
EJEMPLO:
𝒏𝟐+𝟑/𝒏+1
Una sucesión monótona acotada, es
convergente
Una sucesión monótona convergente,
es acotada
SERIES
INFINITAS
TERMINOS
CONSTANTES {sn}
Si la serie infinita Σ ∞ n=1 an es convergente, entonces lim n→∞ an = 0. (*)
Si lim
n→∞ an ≠ 0, entonces Σ ∞ n=1 an es divergente.
La serie de la forma:Σ ∞ n=1 𝑎𝑟𝑛−1 = 𝑎 + 𝑎𝑟 + 𝑎𝑟2+. . . +𝑎𝑟
𝑛−1+ . . .
Se denomina serie geométrica.
POSITIVOS
En una serie convergente de términos positivos, sus términos pueden reagruparse y la serie mantendrá la convergencia.
CRITERIO DE LA RAZÓN
Criterio de convergencia, dado 𝑎𝑛+1 < 𝑎𝑛, ∀𝑛𝜖𝑍
+lim
𝑛→∞ 𝑎𝑛 =0
Σ ∞ n=1 |an|
>1 o ∞ divergente
=1 no se puede concluir
POTENCIA
Una serie de potencias en x-a es una serie de la forma Σ ∞ n=1 𝑐𝑛 𝑥 − 𝑎𝑛 = 𝑐0 + 𝑐1 𝑥 − 𝑎 + 𝑐2 𝑥 − 𝑎2+ . . . +𝑐𝑛 𝑥 − 𝑎𝑛+ . . . Cuando a = 0
TAYLOR
Fórmula de Taylor 𝑓 𝑥 = 𝑓 𝑎 + 𝑓´(𝑎) /1! 𝑥 − 𝑎 + 𝑓´´(𝑎) /2! (𝑥 − 𝑎) 2+. . . + 𝑓 (𝑛) (𝑎) /𝑛! (𝑥 − 𝑎) 𝑛+ 𝑓 (𝑛+1) (𝑧) /(𝑛 + 1)! (𝑥 − 𝑎) 𝑛+1