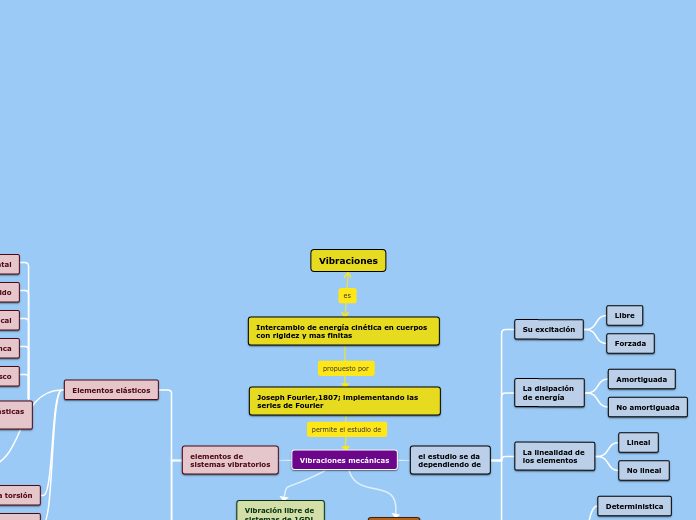
Vibraciones

Intercambio de energía cinética en cuerpos con rigidez y mas finitas

Joseph Fourier,1807; implementando las series de Fourier

Vibraciones mecánicas

el estudio se da
dependiendo de

Su excitación

Libre

Forzada

La disipación
de energía

Amortiguada

No amortiguada

La linealidad de
los elementos

Lineal

No lineal

De la señal

Deterministica

Probabilistica

No periodica

Periodica

Senoidal

Compleja

elementos de
sistemas vibratorios

Elementos elásticos

Elementos elásticos
equivalentes

Serie y paralelo

equivalencias elásticas
torsional

Péndulo horizontal

Péndulo invertido

Péndulo-vertical

Resorte-palanca

Resorte-disco

Resortes helicoidales y a torsión

Elementos estructurales

Elementos inerciales

Masa-palanca

Masa-disco

Elementos amortiguadores

Coulomb

Viscoso

Histéresis

Vibración libre de
sistemas de 1GDL

Vibración libre o
amortiguada

mx''+kx=mg

Vibración libre
amortiguada

Sobreamortiguado

Críticamente
amortiguado

Subamortiguado

Balanceo

Desequilibrio

Equilibrado estático

Máquinas de equilibrado estático

Desequilibrio
y equilibrado

Desequilibrio estático

Balanceado estáticamente
pero no dinámicamente

Máquinas de
equilibrio dinámico

los metodos de
uso general son:

Punto nodal

Bastidor basculante

Comensación mecánica

Rotores rígidos
y fxibles

Rígidos (clase 1)

Cuasi rígidos (clase 2)

Realmente flexibles (clase 3)

Balanceo "INSITU"

1er ensayo

Medir amplitudes en
los cojinetes, debido
a los desequilibrios
originales

2ndo ensayo

Se agrega masa de
ensayo al plano de
correción izquierdo
y se miden amplitudes
en los cojinetes

3er ensayo

Se elimina masa del
ensayo ml y se añade
la masa de ensayo mr
en el plano de corrección
derecho midiendo los
cojinetes nuevamente