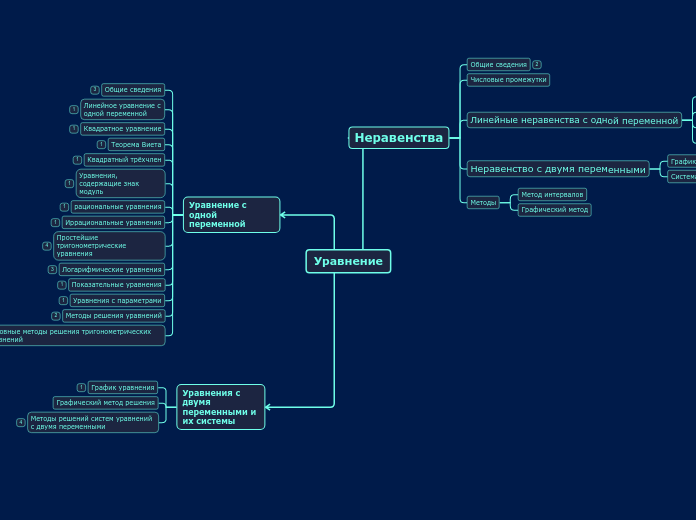
Уравнение
Неравенства
Методы
Графический метод
Метод интервалов
Неравенство с двумя переменными
Система неравенств с двумя переменными
Линейным неравенством с двумя переменными назы&вают неравенство вида ax + by > c или ax + by < c, где x и y — переменные, a, b и c — некоторые числа.
Неравенства вида ax + by>= c и ax + by <= c также
считают линейными. Графиком каждого из неравенств
ax + by >=c и ax + by ,= c, где a^2 + b^2 не = 0, является полуплоскость.
Если a^2 + b^2 = 0, то при с = 0 графиком линейного неравенства является вся координатная плоскость, а при
с не=0 — пустое множество
Если числа а и b не равны нулю одновременно, т. е.
a^2 + b^2 не =0, то графиком линейного неравенства является одна из открытых полуплоскостей (полуплоскость без её
границы), на которые прямая ax + by = c разбивает координатную плоскость xy.
График
Графиком неравенства с двумя переменными называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, координаты которых являются решениями данного неравенства.
Линейные неравенства с одной переменной
Показательные неравенства
Неравенства, содержащие переменную только в показателе степени, называют показательными неравенствами.
Логарифмические неравенства
Если 0 < a < 1, то неравенство logaf(x) > logag(x)
равносильно системе
f(x) < g(x),
f(x) > 0
Если a > 1, то неравенство logaf(x) > logag(x) равно&сильно системе
f(x) > g(x),
g(x) > 0
Квадратные неравенства
Неравенства вида ax2 + bx + c > 0, ax2 + bx + c < 0,
ax2 + bx + c >=0, ax2 + bx + c <= 0, где x — переменная, a, b
и c — некоторые числа, причём a 0, называют квадратными.
Система линейных неравенств
Решением системы неравенств с одной переменной
называют значение переменной, которое обращает каждое неравенство системы в верное числовое неравенство
Если требуется найти все общие решения двух или нескольких неравенств, то говорят, что надо решить систему неравенств.
Неравенства вида ax > b, ax < b, ax>= b, ax <= b, где x —переменная, a и b — некоторые числа, называют линейными неравенствами с одной переменной.
Числовые промежутки
Все решения неравенства образуют множество решений неравенства. Если неравенство решений не имеет, то множество его решений является пустым.
Решением неравенства с одной переменной называют значение переменной, которое обращает его в верное числовое неравенство
Уравнения с двумя переменными и их системы
Методы решений систем уравнений с двумя переменными
подтема
Метод замены переменных
Метод сложения
Метод подстановки
Графический метод решения
График уравнения
Графиком уравнения с двумя переменными называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, координаты которых (пары чисел) являются решениями данного уравнения.
Уравнение с одной переменной
Основные методы решения тригонометрических уравнений
Применение ограниченности тригонометрических
функций
Введение вспомогательного угла
Ввод новой переменной
Методы решения уравнений
Разложение на множители
метод замены переменной
Уравнения с параметрами
Рассмотрим линейное уравнение ax = 1 Если a = 0, то данное уравнение корней не имеет. Если
a не = 0, то уравнение имеет единственный корень x =1/а .
Решая это уравнение, мы придавали буквам a и x разный смысл: буква x играла роль неизвестного числа, а буква a — роль известного числа. В таких случаях говорят, что a является параметром, а само уравнение называют уравнением с параметром.
Показательные уравнения
Уравнения, в которых переменная содержится только
в показателе степени, называют показательными уравнениями.
Логарифмические уравнения
Пусть a > 0, a не =1. Уравнение вида loga f(x) =
= loga g(x) равносильно любой из систем
f(x) = g(x),
g(x) > 0
f(x) = g(x),
f(x) > 0
Простейшие тригонометрические уравнения
Уравнение сtg x = b
Уравнение tg x = b
Уравнение cos x = b
Уравнение sin x = b
Иррациональные уравнения
Уравнения, содержащие переменную под знаком корня, называют иррациональными.
рациональные уравнения
Уравнение, левая и правая части которого являются рациональными выражениями, называют рациональным.
Уравнения, содержащие знак модуль
Если a >=0, то уравнение вида | f(x) | = a равносильно совокупности
f(x) = a,
f(x) = –a.
Квадратный трёхчлен
Квадратным трёхчленом называют многочлен вида
ax2 + bx + c, где x — переменная, a, b и c — некоторые числа, причём a не равно 0.
Теорема Виета
Теорема Виета. Если x1 и x2 — корни квадратного
уравнения ax2 + bx + c = 0, то
x1 + x2 = -b/a ; x1x2 =c/a .
Квадратное уравнение
Квадратным уравнением называют уравнение вида ax2 + bx + c = 0, где x — переменная, a, b, c — некоторые числа, причём a не равно 0.
Линейное уравнение с одной переменной
Уравнение вида ax = b, где x — переменная, a и b —
некоторые числа, называют линейным уравнением с одной переменной.
Общие сведения
Областью определения уравнения f(x) = g(x) называют множество значений переменной x, при которых имеют смысл обе части уравнения.
Решить уравнение — это значит найти множество его
корней.
Корнем уравнения называют значение переменной,
обращающее уравнение в верное числовое равенство