Уравнения и неравенства

Plus de détails

Cенсорные системы

par Nik Kasyanov

Воспитательный процесс как система

par Marina Zaikova

2/4. Как разработать наиболее эффективный способ выделения ДНК для домашних условий?

par Valery Zaitsev

Уравнение

par Светлана Попова

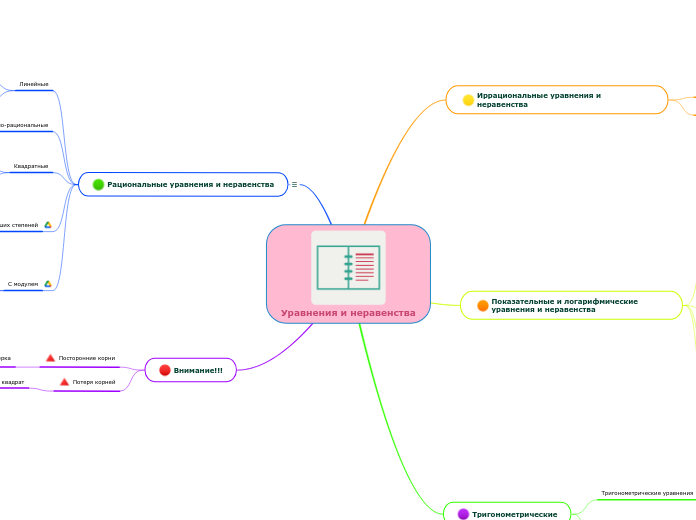
Уравнения и неравенства

Внимание!!!

Потеря корней

Возведение в квадрат

Посторонние корни

Проверка

Рациональные уравнения и неравенства

Теорема 1. Если какое-либо слагаемое перенести из одной части уравнения в другую часть с противоположным знаком, то получим уравнение, равносильное исходному. Если какое-либо слагаемое перенести из одной части неравенства в другую с противоположным знаком, то получим неравенство, равносильное исходному.

Теорема 2. Если к обеим частям данного уравнения прибавить (или вычесть) одно и то же число, то получим уравнение, равносильное исходному. Если обе части неравенства умножить (разделить) на одно и то же положительное число (или на одну и ту же функцию, имеющую смысл и положительную на области определения исходного неравенства), то получим неравенство, равносильное исходному.

Теорема 3. Если обе части уравнения умножить (или разделить) на одно и то же отличное от нуля число (или на одну и ту же функцию, имеющую смысл и не равную нулю на области определения исходного уравнения), то получим уравнение, равносильное исходному. Если обе части неравенства умножить (разделить) на одно и то же отрицательное число (или на одну и ту же функцию, имеющую смысл и отрицательную на области определения исходного неравенства), изменив при этом знак неравенства на противоположный, то получим неравенство, равносильное исходному.

Теорема 4. При возведении обеих частей уравнения в нечетную натуральную степень получается уравнение равносильное исходному. В случае, когда обе части уравнения неотрицательные на области определения, при возведении обеих его частей в четную натуральную степень получается уравнение, равносильное исходному. При возведении обеих частей неравенства в нечетную натуральную степень с сохранением знака неравенства получается неравенство равносильное исходному. В случае, когда обе части неравенства неотрицательные на области определения, при возведении обеих его частей в четную натуральную степень с сохранением знака неравенства получается неравенство, равносильное исходному. 

Уравнение, левая и правая части которого являются рациональными выражениями, называют рациональным.

Неравенства называются равносильными, если множества их решений равны.

С модулем

Неравенства с модулем

Уравнения с модулем

Уравнения высших степеней

Однородные уравнения

Возвратные уравнения

Метод введения новой переменной

Метод разложения на множители

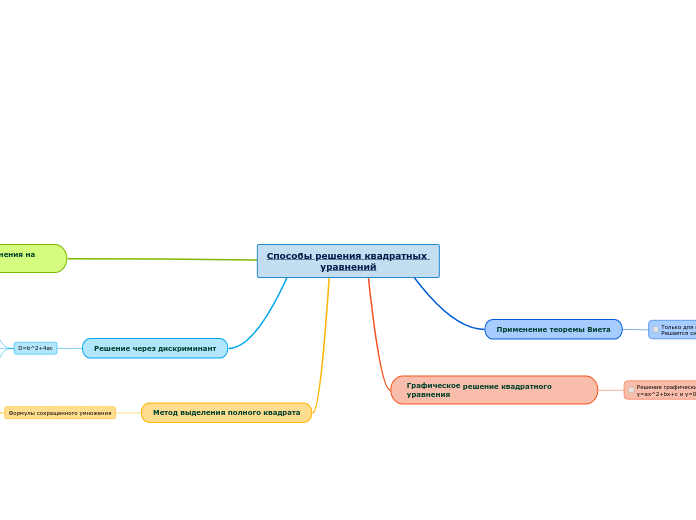
Квадратные

Квадратные неравенства

Квадратные уравнения

Дробно-рациональные

Дробно-рациональные неравенства

Дробно-рациональные уравнения

Линейные

Линейные неравенства

Линейные уравнения

Тригонометрические

Тригонометрические неравенства

Методы решения тригонометрических неравенств

при помощи числовой окружности

при помощи графиков соответствующих функций

Тригонометрические уравнения

Методы решения тригонометрических уравнений:

метод введения вспомогательного аргумента

универсальная подстановка

метод решения однородных тригонометрических уравнений,

метод введения новой переменной

метод разложения на множители

Показательные и логарифмические уравнения и неравенства

Логарифмические неравенства

Логарифмические уравнения

При решении логарифмических уравнений используются такие методы, как:

- определение логарифма числа, операции логарифмирования или потенцирования

Показательные неравенства

Показательные уравнения

При решении показательных уравнений используются такие методы, как:

и др

- определение логарифма числа, операции логарифмирование или потенцирование

- метод решения однородных уравнений;

- метод разложения на множители;

- метод введения новой переменной;

Иррациональные уравнения и неравенства

Иррациональные неравенства

Иррациональные уравнения