Тригонометрические функции y=sinx, y=cosx, y=tgx, y=ctgx.

Plus de détails

Конструкторы веб-сайтов

par Милодан Алина

Типы данных С#

par Таня Михайлова

Тригонометрия

par Яна Лазовская

Типы данных в С#

par Кирилл Филиппов

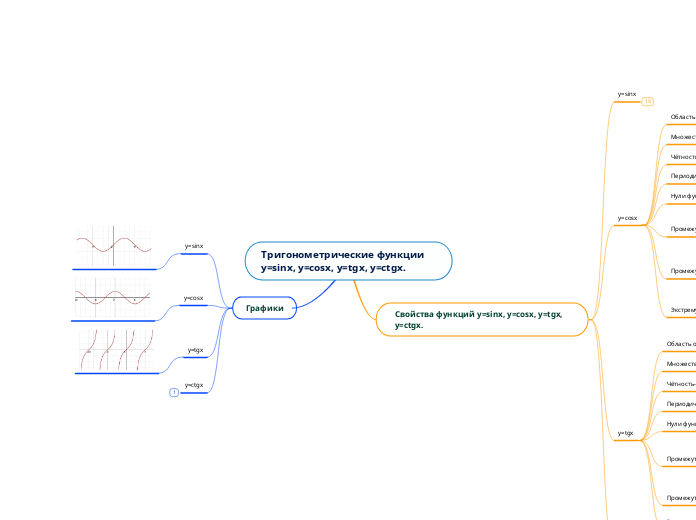
Тригонометрические функции y=sinx, y=cosx, y=tgx, y=ctgx.

Графики

Свойства функций y=sinx, y=cosx, y=tgx, y=ctgx.

y=ctgx

Функция убывает на каждом интервале, целиком принадлежащем её области определения.

ctgx=0, при х=п/2+n, n принадлежит Z

Функция периодическая , период равен п: ctg(a+п)=ctg(a)

E(y=ctgx)=R

D(y=ctgx)=R

y=tgx

Нет

Функция возрастает на каждом интервале, целиком принадлежащем её области определения

tgx=0, при x=пи*n, n принадлежит Z

Функция периодическая с основным периодом T=2пи

функция нечётная

E(tg x)=R

D(tg x)=R\{/2+n(n принадлежит Z)}

y=cosx

cosx=0, при x=пи/2+-пи*n, n принадлежит Z.

Функция периодичность с основным периодом Т=2

Функция чётная

E(cosx)=[-1,1]

D(cosx)=R

y=sinx

Экстремумы

Промежутки монотонности

Промежутки знакопостоянства

Нули функции

sin x = 0 , при x=+-пи*n, n принадлежит Z.

Периодичность

Функция периодическая с основным периодом Т=2

Чётность-нечётность

Функция нечётная

Множество значений

E(cos x)= [-1, 1]

Область определения

D(cos x) = R