par lorena luis Il y a 4 années
334
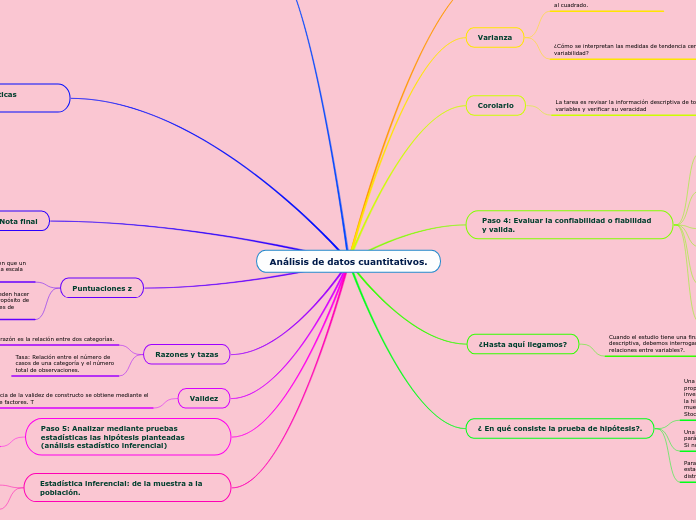
Análisis de datos cuantitativos
En el campo del análisis de datos cuantitativos, es crucial comprender las características y la distribución de los datos recopilados. Las estadísticas descriptivas, como asimetría y curtosis, ayudan a comparar la distribución de los datos con la curva normal teórica, permitiendo identificar dónde se concentran las puntuaciones.