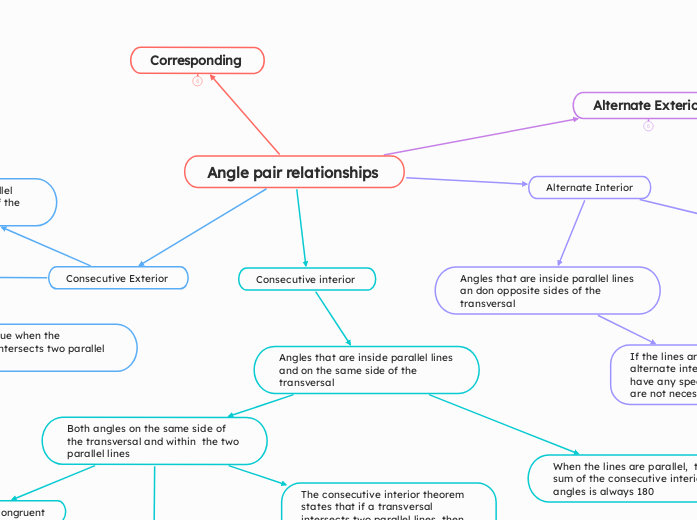
Angle pair relationships
Consecutive interior
Angles that are inside parallel lines and on the same side of the transversal
When the lines are parallel, the sum of the consecutive interior angles is always 180
Both angles on the same side of the transversal and within the two parallel lines
Not necessarily congruent
The consecutive interior theorem states that if a transversal intersects two parallel lines, then the consecutive interior angles are supplementary
Consecutive Exterior
Supplementary ( add up to 180 )
Consecutive refers to things that appear next to eachother
Only holds true when the transversal intersects two parallel lines
Angles that are outside parallel lines and on the same side of the transversal
Alternate Interior
Congruent when the line intersected by the transversal are parallel
Located on the inside of the the two parallel lines, but on opposite sides of the transversal
Only applies when a transversal intersects two lines
Angles that are inside parallel lines an don opposite sides of the transversal
If the lines are not parallel, alternate interior angles do not have any special properties and are not necessary congruent
Alternate Exterior
They are situated on the exterior of the two parallel lines, meaning outside the line where they intersect
When two parallel lines are cut by transversal, the alternate Exterior angles are always congruent to each other
The property of being congruent only applies when two lines being intersected b y the transversal are parallel
Located on opposite sides of the transversal line
Angles that are outside parallel lines and on opposite sides of the transversal
Corresponding
forms when a transversal intersects two parallel lines
occuppy there same relative position at each intersection
Congruent
Angles that are in the same spot, different line
Located on the same side of the transversal