par Carlos Varon Il y a 2 années
155
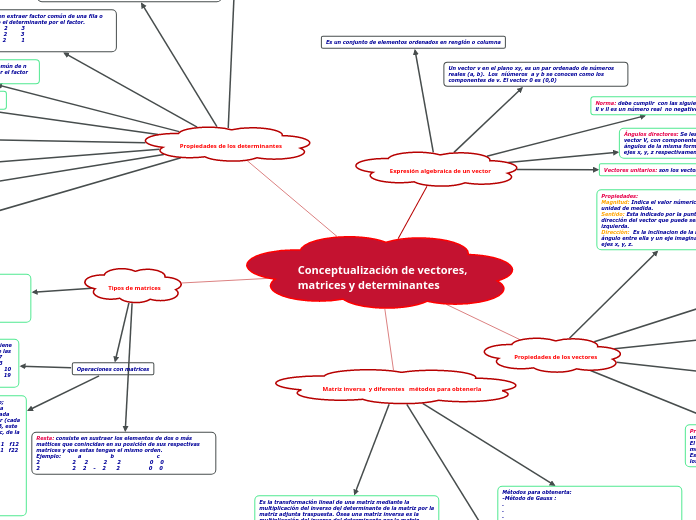
Conceptualización de vectores, matrices y determinantes
Las matrices son estructuras matemáticas fundamentales en el álgebra lineal que se utilizan para representar sistemas de ecuaciones y transformaciones lineales. Existen diversos tipos de matrices, como la matriz inversa, la matriz nula, la matriz traspuesta, la matriz rectangular, la matriz columna y la matriz fila.