par LUZ MARINA BOHORQUEZ MARTINEZ Il y a 8 années
818
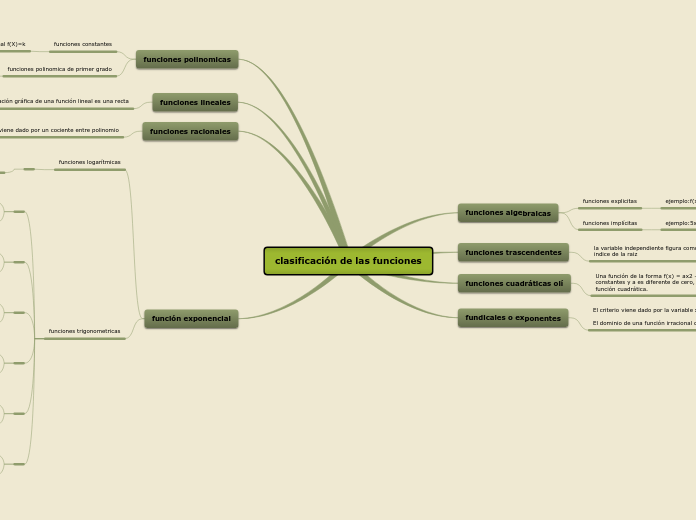
Derivadas trascendentes
The calculation of derivatives for various types of functions, including trigonometric, exponential, logarithmic, hyperbolic, and their inverses, is explored. Understanding the derivatives of trigonometric functions such as sine, cosine, tangent, cotangent, secant, and cosecant requires a fundamental grasp of the definitions of sine and cosine, particularly in relation to angles measured in radians.