par Diana Matos Il y a 8 années
299
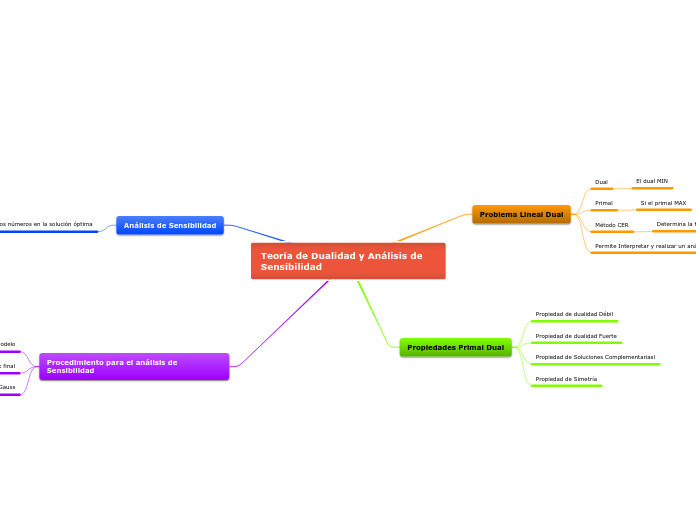
Dualidad y Análisis de Sensibilidad
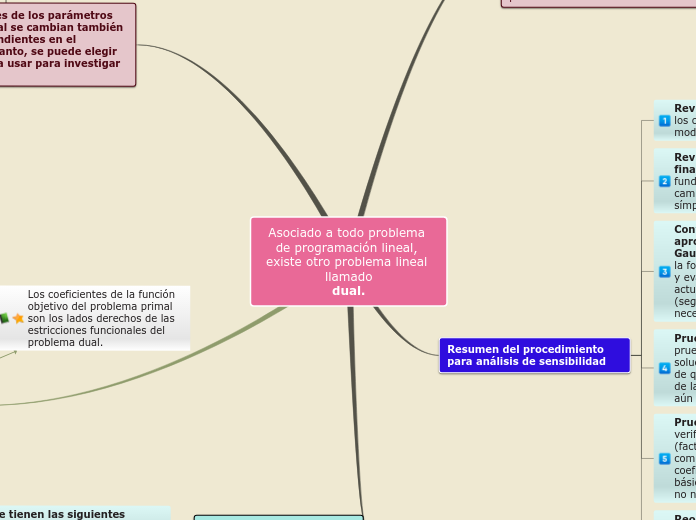
The relationship between primal and dual problems in linear programming is characterized by specific properties and interactions. Duality describes how the constraints and objective functions of the primal and dual problems are interrelated.