par José Daniel Ortiz Cruz Il y a 12 mois
85
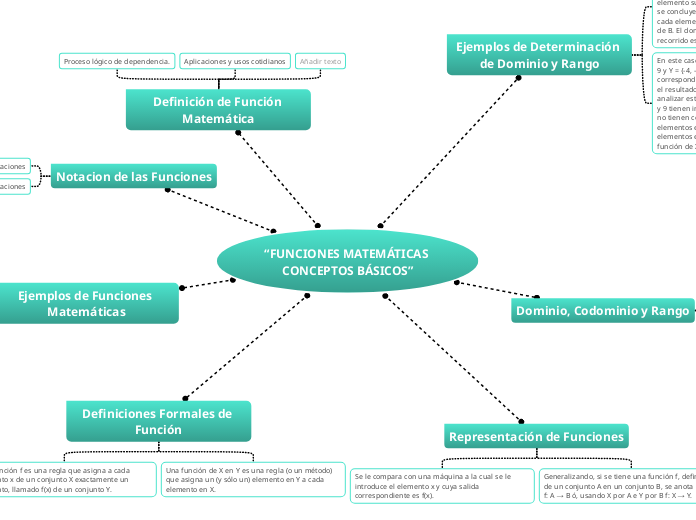
“FUNCIONES MATEMÁTICAS CONCEPTOS BÁSICOS”
Una función matemática es una regla que asigna a cada elemento de un conjunto de entrada un único elemento de un conjunto de salida. Esta relación de dependencia lógica se aplica en diversas situaciones cotidianas y científicas, como calcular el peso de empleados en una oficina o aplicar reglas matemáticas específicas como elevar un número al cuadrado.