Fundamentos de sistemas y tecnologías de información

Plus de détails

Las sucesiones numéricas y las progresiones.

par Irene Sancho Ferrándiz

RECONOMIENTO DE UN EQUIPO TECNOLÓGICO

par ANA JAVIER MACHUCA

Lógica matemática y conjuntos

par Familia Santacruz Sevilla

DISCO

par Jared Zaith

PUNTO DEL PLANO COMPLEJO

REGIONES

INFINITO

Los conjuntos finitos tienen una propiedad "intuitiva" que los caracteriza: "dada una parte propia de los mismos, esta contiene un número de elementos menor que todo el conjunto". Es decir, no puede establecerse una biyección entre una parte propia del conjunto finito y todo el conjunto

Técnicamente es la proyección estereográfica de los números complejos ampliados con el ∞, donde se define una nueva distancia para obtener una topología. Lo que tiene aplicaciones en geometría algebraica, teoría de la relatividad o mecánica cuántica y sirve para visualizar la 4ª dimensión

ACOTAMIEMTO

existe una sierta vecindad del origen que encierra totalmente a S.

DOMINIO

Subtopic

CONVEXA

como conjunto conexo, cuando en el conjuto S los puntos que la conforman se pueden conectar mediante una linae recta poligonal que consite en un numero finito de segmentos.

CONJUNTO CERRADO

Cuando el conjunto S contiene puntos interior y puntos frontera.

UNA CIRCUFERENCIA

circunferencia es una línea curva, cerrada y plana, cuyos puntos están todos a la misma distancia de otro punto, llamado centro. |Z-Z0||=P Z=PUNTOS DE LA CIRCUFERENCIA Z0=CENTRO DE LA CIRCUFERENCIA P=RADIO.

CONJUTO ABIERTO

que es un conjunto abierto cuando cada unos de los puntos S de un conjunto es un punto interior.

VECINDAD

Como vecindad del punto Z0, que está en el plano complejo, a todo conjunto V que contiene un círculo abierto V(Z0,P) = {z / |z-Z0 | < P}, de centro Z0 y radio P> 0. El círculo V(Z0,P ) es, obviamente, una vecindad de Z0

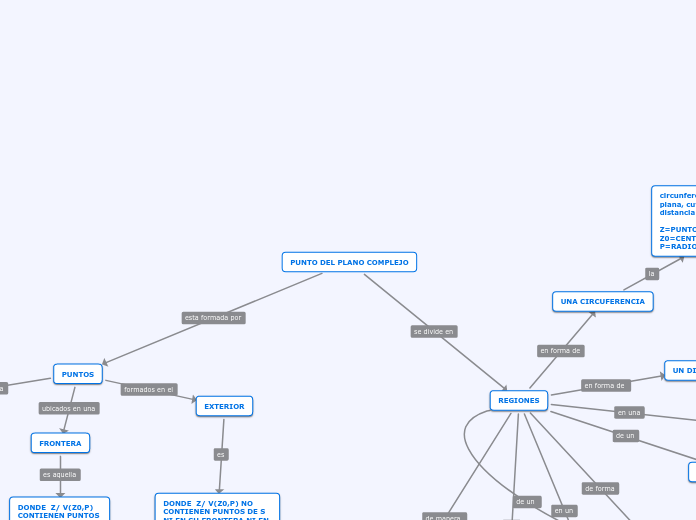
SE CONFORMA EN DOS

De la forma 0<|Z-Z0||˂P

VECIDAD COMPLEJA

De la forma |Z-Z0||˂P

UN DISCO

cuando su conjuto S esta conformado por puntos interiores,puntos fronteras y ademas de esto esta formado por puntos exteriores.

PUNTOS

FRONTERA

DONDE Z/ V(Z0,P) CONTIENEN PUNTOS DENTRO Y FUERA DE LA REGION S

EXTERIOR

DONDE Z/ V(Z0,P) NO CONTIENEN PUNTOS DE S NI EN SU FRONTERA NI EN SU INTERIOR.

INTERIOR

TODOS AQUELLOS PUNTOS Z0 CONTIENEN UNA VECINDAD. |Z||˂P |Z-Z0||˂P TOTALMENTE CONTENIDO EN EN S.