GEOMETRÍA ANALÍTICA, LINEAS RECTAS Y CIRUNFERENCIAS

Plus de détails

Potencial de membrana en reposo

par Nicolle Arevalo

CAD Y CAM

par Tomas Aranda

Historia de la Topografía

par Ander Sanchez Lopez

Diseño Agrícola Asistido por Computadora

par Daniel Rojas

GEOMETRÍA ANALÍTICA, LINEAS RECTAS Y CIRCUNFERENCIAS

CONICAS

HIPERBOLA

Es el lugar geométrico de los puntos del plano cuya diferencia de distancias a dos puntos fijos llamados focos es constante

RELACIONES ENTRE LOS SEMIEJES:

ASINOTAS:Son las rectas de ecuaciones:

EJE DE SIMETRÍA:Son las rectas que contienen al eje real o al eje imaginario

EJE MAYOR:Es el segmento de longitud 2a

DISTANCIA FOCAL: Es el segmento de longitud 2c

RADIOS VECTORES:Son los segmentos que van desde un punto de la hipérbola a los focos: PF y PF'

VÉRTICES:Los puntos A y A' son los puntos de intersección de la hipérbola con el eje focal.Los puntos B y B' se obtienen como intersección del eje imaginario con la circunferencia que tiene por centro uno de los vértices y de radio c

EJE SECUNDARIO O IMAGINARIO:Es la mediatriz del segmento FF'

EJE PRINCIPAL O REAL:Es la recta que pasa por los focos

ELIPSE

EJEMMPLO

Es el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos llamados focos es constante

CENTRO DE SIMETRÍA:Coincide con el centro de la elipse, que es el punto de intersección de los ejes de simetría

EJE DE SIMETRÍA: Son las rectas que contienen al eje mayor o al eje menor

EJE MENOR:Es el segmento segmento de longitud 2b, b es el valor del semieje menor

EJE MAYOR:Es el segmento segmento de longitud 2a, a es el valor del semieje mayor

VÉRTICES : Son los puntos de intersección de la elipse con los ejes: A, A', B y B'

DISTANCIA FOCAL:Es el segmento segmento de longitud 2c, c es el valor de la semidistancia focal

RADIOS VECTORES:Son los segmentos que van desde un punto de la elipse a los focos: PF y PF'

CENTRO:Es el punto de intersección de los ejes

EJE SECUNDARIO:Es la mediatriz del segmento FF'

EJE FOCAL:Es la recta que pasa por los focos

FOCOS:Son los puntos fijos F y F'

PARÁBOLA

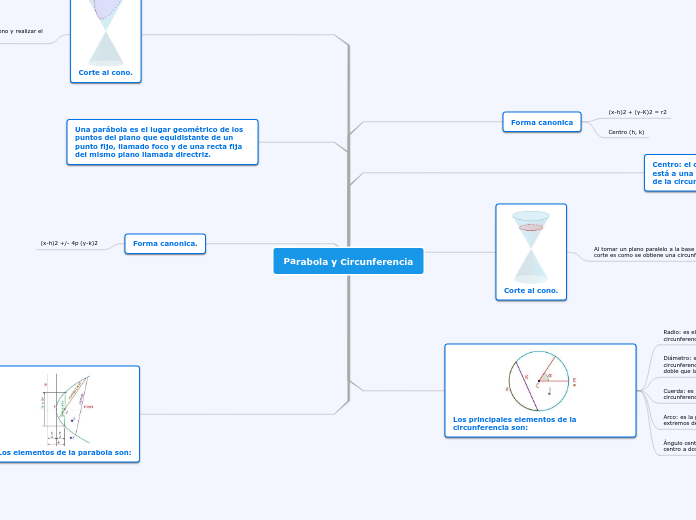
ECUACIÓN CANÓNICA

se define como el lugar geométrico de los puntos del plano que equidistan de un punto denominado foco, y una recta denominada directriz.El eje de la parábola es la recta perpendicular a la directriz, que pasa por el foco F. La distancia FD, del foco a la directriz, se denomina parámetro de la parábola, el punto medio del segmento FD, es el punto V, que se denomina vértice de la parábola.

RADIO VECTOR:Es el segmento que une un punto cualquiera de la parábola con el foco

VÉRTICE:Es el punto medio entre el foco y la directriz. También se puede ver como el punto de intersección del eje con la parábola

EJE:La recta perpendicular a la directriz y que pasa por el foco recibe el nombre de eje. Es el eje de simetría de la parábola

PARÁMETRO:A la distancia entre el foco y la directriz de una parábola se le llama parámetro p

DIRECTRIZ:Es la recta fija D

FOCO:Es el punto fijo F

CIRCUNFERENCIA

EJEMPLO

ECUACIÓN CANONICA

se puede definir como la figura generada por una curva cerrada o perímetro en el cual no hay vértice ni ángulos internos.La circunferencia es una línea curva, cerrada y plana, cuyos puntos están todos a la misma distancia de otro punto, llamado centro.

RECTA TANGENTE:recta que toca a la circunferencia en un solo punto y es perpendicular a un radio

RECTA SECANTE:recta que corta dos puntos cualesquiera de una circunferencia

DIÁMETRO:mayor cuerda que une dos puntos de una circunferencia. Hay infinitos diámetros y todos pasan por el centro de la circunferencia

CUERDA:pedazo de recta que une dos puntos cualquiera de una circunferencia

RADIO:pedazo de recta que une el centro con cualquier punto perteneciente a la circunferencia

CENTRO:punto central que está a la misma distancia de todos los puntos pertenecientes a la circunferencia