par Daniela Fernandez Il y a 6 années
1946
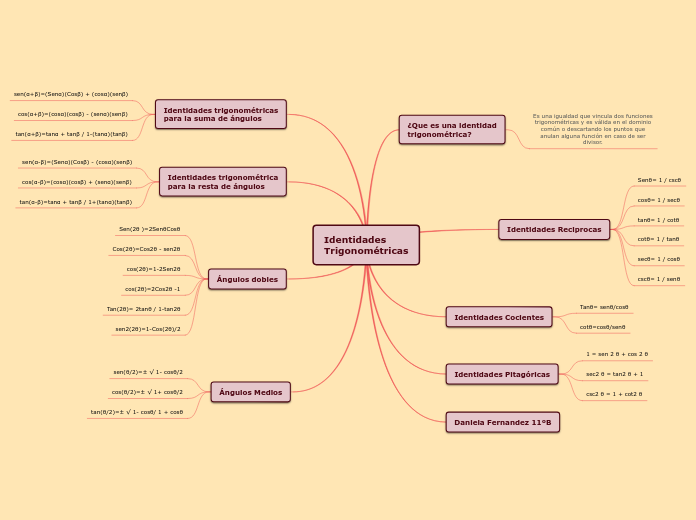
Identidades Trigonométricas
Las identidades trigonométricas son ecuaciones que relacionan funciones trigonométricas y son válidas en su dominio común. Existen varias categorías de estas identidades, incluyendo las recíprocas, para la suma y resta de ángulos, para ángulos medios, pitagóricas, y cocientes.