par Nicolas Ramirez Rodriguez Il y a 8 années
898
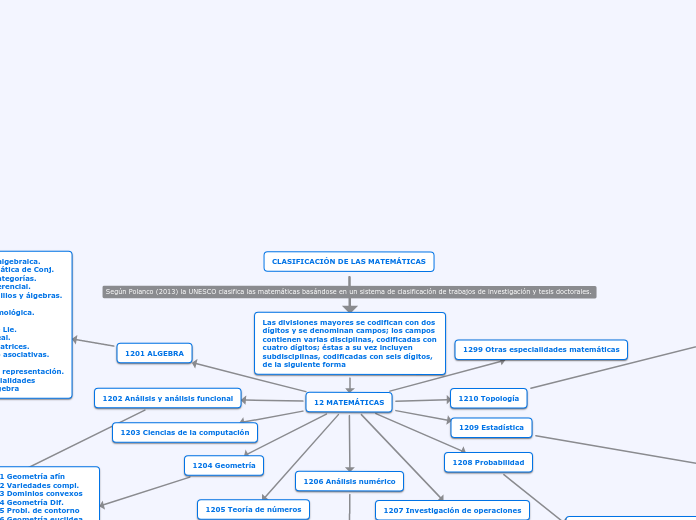
importancia de los numeros en las diferentes ramas de la ciencia
El estudio de los números abarca varias ramas de la ciencia, cada una con su enfoque particular y aplicaciones específicas. La teoría combinatoria de números se centra en problemas que combinan ideas de la teoría de números con formulaciones combinatorias, abarcando temas como sistemas cubiertos y progresiones aritméticas.