INTRODUCCIÓN A LA PROBABILIDAD
Definición de probabilidad
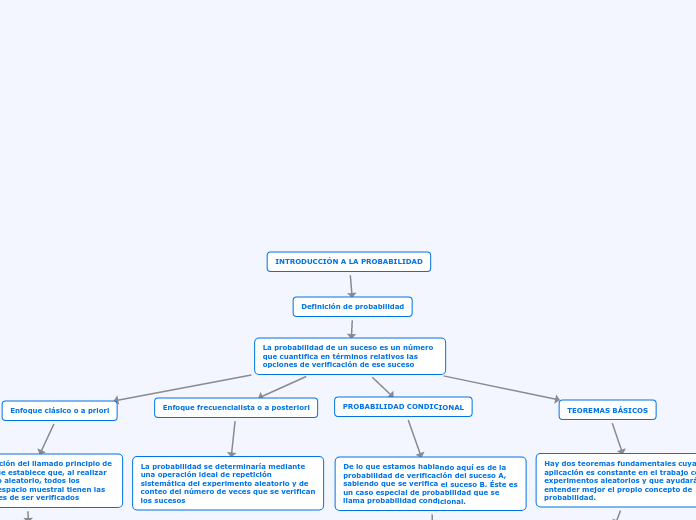
La probabilidad de un suceso es un número que cuantifica en términos relativos las opciones de verificación de ese suceso
TEOREMAS BÁSICOS
Hay dos teoremas fundamentales cuya aplicación es constante en el trabajo con experimentos aleatorios y que ayudarán a entender mejor el propio concepto de probabilidad.
Teorema del producto
El segundo teorema se refiere a la probabilidad de la intersección de dos sucesos en un caso especial, de alto interés para nosotros y que exige la definición previa del concepto de independencia
Dos sucesos, A y B, son independientes si la verificación de uno no altera la probabilidad del otro.
Es decir, Si P(A | B) = P(A) entonces, A y B son sucesos independientes
Teorema de la adición
Empezaremos por definirlo y luego lo explicaremos e ilustraremos con algún ejemplo
Según el teorema de la adición, la probabilidad de la unión de dos sucesos es igual a la suma de sus probabilidades menos la probabilidad de su intersección:
P(A ∪ B) = P(A) + P(B) − P(A ∩ B)
PROBABILIDAD CONDICIONAL
De lo que estamos hablando aquí es de la probabilidad de verificación del suceso A, sabiendo que se verifica el suceso B. Éste es un caso especial de probabilidad que se llama probabilidad condicional.
se representa por P (A | B) y se lee «probabilidad de A, dado B». Es fácil demostrar que esa probabilidad se puede obtener a partir de las probabilidades de la intersección de esos sucesos y de la condición impuesta. En términos generales:
La probabilidad de un suceso, A, dada la verifi cación de otro suceso, B, se llama probabilidad condicional de A dado B, y es igual a la probabilidad de su intersección dividida por la probabilidad de la condición. Es decir:
P(A | B) =
P(A ∩ B)
----------------
P(B)
Enfoque frecuencialista o a posteriori
La probabilidad se determinaría mediante una operación ideal de repetición sistemática del experimento aleatorio y de conteo del número de veces que se verifican los sucesos
Enfoque clásico o a priori
exige la aceptación del llamado principio de indiferencia, que establece que, al realizar un experimento aleatorio, todos los elementos del espacio muestral tienen las mismas opciones de ser verificados
Desde el enfoque clásico o a priori, que exige asumir el principio de indiferencia, se define la probabilidad de un suceso como la frecuencia relativa de ese suceso en el espacio muestral.
Probabilidad de un suceso =
Número de casos favorables
-----------------------------------------
Número de casos posibles