par Juan Numpaque Cabezas Il y a 3 années
226
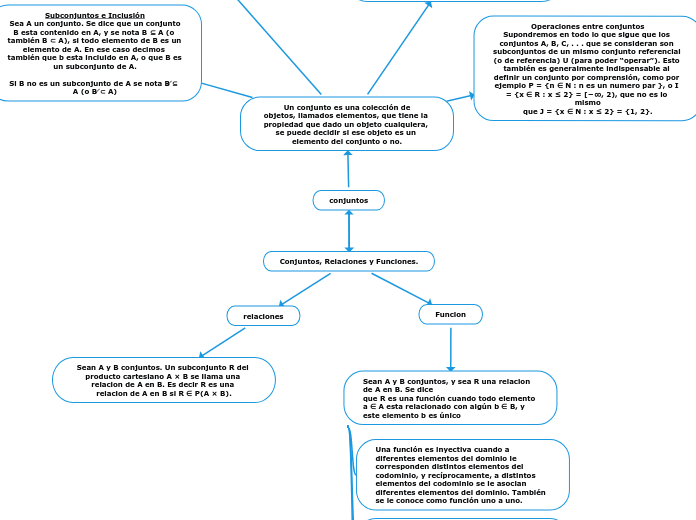
mapa conceptual 3
Los conjuntos son colecciones de elementos que permiten determinar si un objeto pertenece o no a ellos. Un subconjunto es un conjunto cuyos elementos están contenidos en otro conjunto mayor.