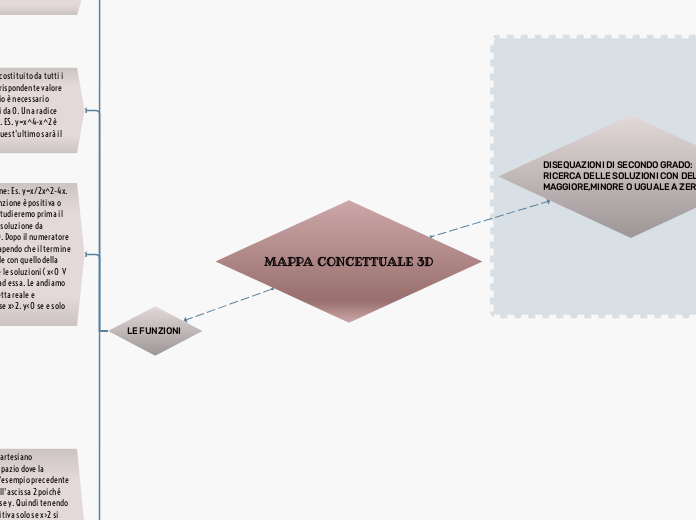
MAPPA CONCETTUALE 3D
LE FUNZIONI
Grafico: si disegna un grafico cartesiano delimitando con delle rette lo spazio dove la funzione esiste. Utilizzando l'esempio precedente occorre disegnare una retta sull'ascissa 2 poiché quella sullo 0 coincide con l'asse y. Quindi tenendo presente che la funzione è positiva solo se x>2 si elimina la parte del quadrante negativo. Sappiamo che è negativa solo ed esclusivamente quando x è minore di 0 (elimineremo perciò la parte positiva) e quando x è compreso tra 0 e 2 dove eseguiremo la stessa operazione di prima. Concluderemo quindi che la funzione si svilupperà nelle parti non eliminate.
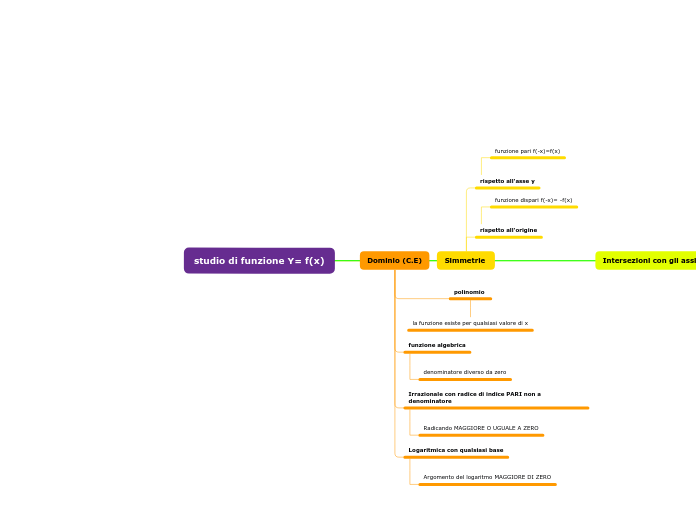
Intersezioni con gli assi: Per trovare le intersezioni con gli assi abbiamo proceduto in questa maniera: data una funzione y=x/2x^2-4x poniamo, la x=o per trovare l'intersezione con l'asse y e per trovare l'intersezione con x poniamo tutta la funzione uguale a 0. Sull'asse x le intersezioni sono 0 e 2 mentre sull'asse y non ve ne sono.
Definizione di una funzione pari e di una dispari: Se f(-x)= f(x) allora la funzione è pari. E' dispari solo quando f(-x)=-f(x). Es. di una funzione pari è quando il grafico della medesima è simmetrico rispetto all'asse y . E' dispari quando è simmetrico rispetto all'origine.
Una funzione si dice iniettiva e suriettiva se ogni elemento di Y ha al massimo una controimmagine in X . Una funzione si dice biiettiva se è sia iniettiva sia suriettiva.
Lettura di un grafico :abbiamo svolto infine quest'ultimo esercizio introducendo anche nuovi concetti. Abbiamo parlato di " zeri della funzione" che otteniamo quando questa interseca l'asse x e delle soluzioni di una possibile equazione :es. f(x)=-2. Si disegna sul grafico una retta parallela all'asse delle ascisse passante per il punto (in questo caso -2) in questione sull'asse y e si verifica il numero di punti intersecati dalla retta.
Una funzione si dice strettamente crescente se x1 f(x2) per ogni x1,x2 E . Si dice costante se f(x1)= f(x2) per ogni x1,x2 E I. Una funzione si dice invece crescente in senso lato se x1
Studio del segno di una funzione: Es. y=x/2x^2-4x. Dobbiamo sapere quando la funzione è positiva o negativa ponendo y> o < di 0 .Studieremo prima il numeratore verificando che la soluzione da rappresentare sulla retta è x>0. Dopo il numeratore studiamo il denominatore e, sapendo che il termine al quadrato ha il segno concorde con quello della disequazione verifichiamo che le soluzioni( x<0 V x >2) saranno sempre esterne ad essa. Le andiamo quindi a rappresentare sulla retta reale e verifichiamo che y>0 se e solo se x>2. y<0 se e solo se x<0 V 0
Dominio: si intende l'insieme costituito da tutti i numeri reali che hanno un corrispondente valore f(x). Per determinare il dominio è necessario imporre i denominatori diversi da 0. Una radice cubica è sempre verificata in R. ES. y=x^4-x^2 è sempre verificata in R quindi quest'ultimo sarà il dominio.
Una funzione si dice inversa se e solo se è iniettiva ,si indica con f di -1 perché funzione inversa di f e perché associa a ciascun elemento dell'immagine di f la sua unica controimmagine.
Insieme immagine: quando vi sono gli elementi del codominio che risultano anche essere immagine di almeno un elemento del dominio. IM (f)=( y E B/ esiste x E A/ f(x)= y). Perciò prendendo l'esempio d un punto con coordinate cartesiane (3;-3) l'immagine di 3 sarà -3.
Dati due insiemi A e B si dice funzione una relazione che associa a ogni elemento di A un solo elemento di B. Le abbiamo classificate in razionali e razionali fratte.
La legge che definisce una funzione f di variabile reale ,viene solitamente assegnata con un'equazione del tipo y= f(x). Possiamo inoltre determinare i valori assunti dalla funzione ponendo la x sotto un valore arbitrario. ES.1: 5x-6x^2 con x=1.Si sostituisce 1 alla x per determinare il valore y quando appunto la x è pari a 1. In questo caso la soluzione è pari a -1.
DISEQUAZIONI DI SECONDO GRADO: RICERCA DELLE SOLUZIONI CON DELTA MAGGIORE,MINORE O UGUALE A ZERO
Caso 3
Δ< 0: non vi sono soluzioni in R. Non è possibile avere una quantità sotto radice negativa.
Caso 2:
Δ=0: le soluzioni saranno reali e coincidenti. Se il segno di a è concorde con il segno della disequazione troviamo che: con x1 diverso da x2 sia che la disequazione sia larga sia che sia stretta è sempre verificata in R.
Caso 1:
Δ>0 : le soluzioni saranno sempre reali e distinte. Posto ax^2+bx+c> 0 verifichiamo che il trinomio risulta positivo per valori esterni poiché il segno di a è concorde con il segno della disequazione. Ove il segno di a fosse discorde con quello della disequazione, quest'ultima è verificata per valori interni ad essa. ES: 5x^2+ 6x+1 > 0 il delta è maggiore di 0, il segno del termine al quadrato è concorde con quello della disequazione quindi le soluzioni (-1/5 e 1)saranno valori esterni . ES.2: -5x^2+6x+1 > 0. Osserviamo che il segno di a è discorde con quello della disequazione perciò considerando anche il fatto che il delta è maggiore di 0, essa sarà verificata per valori interni.