mate normal

Plus de détails

Teoria del Estudio Independiente

par Salomon Urriago

LA APERTURA DE LA SUCESION

par Gaby Mesones

Probabilidad: Conceptos básicos

par Javier González

SUCESIÓN

par Daniel Sánchez

matemática del tronco común

parábola y elipse

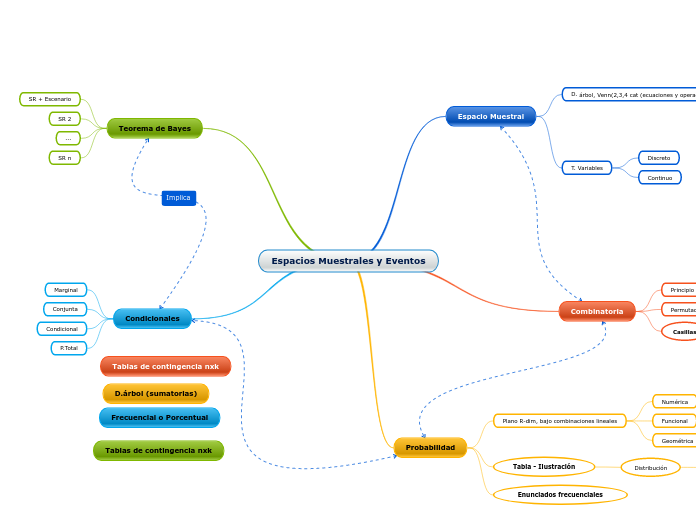
elipse

La elipse es el lugar geométrico de los puntos del plano cuya suma de las distancias a los dos focos (puntos interiores fijos F1 y F2) es constante. Es decir, para todo punto a de la elipse, la suma de las distancias d1 y d2 es constante.

parabola

Una parábola es el lugar geométrico de los puntos del plano que equidistan de un punto fijo, llamado foco y de una recta fija del mismo plano llamada directriz. Dibujo de la parábola como producto de la intersección del cono con un plano. La parábola es una sección cónica, resultado de la intersección de un cono recto con un plano que corta a la base del mismo, oblicuo a su eje y paralelo a una generatriz g de la superficie cónica. El foco y la directriz determinan cómo va a ser la apariencia de la parábola (en el sentido de que “parecerá” más o menos abierta según sea la distancia entre F y la directriz). Todas las parábolas son semejantes. Su excentricidad es 1 en todos los casos. Solamente varía la escala.

Los elementos de la parábola son: Dibujo de los elementos de una parábola: del foco, directriz, radio vector y eje Foco: el foco F es el punto fijo. Los puntos de la parábola equidistan del foco y la directriz. Directriz: es la recta fija D. Los puntos de la parábola equidistan de la directriz y el foco. Radio vector: es el segmento R que une el foco con cada uno de los puntos de la parábola. Es igual al segmento perpendicular a la directriz desde el punto correspondiente. Eje: es la recta E perpendicular a la directriz que pasa por el foco y el vértice. Es el eje de simetría de la parábola. Dibujo de los elementos de una parábola: del parámetro, vértice y puntos interiores y exteriores Parámetro: es el vector p, que va desde el foco al punto más próximo de la directriz. Es importante el signo del parámetro. En las parábolas verticales, cuando el parámetro es positivo la parábola se abre hacia arriba. Cuando p es negativo, la parábola se abre hacia abajo. Igualmente, en las parábolas horizontales, cuando p es positivo, se abre hacia la derecha y cuando p es negativo, la parábola se abre a la izquierda. Vértice: es el punto V de la intersección del eje y la parábola. Distancia focal: distancia entre el foco F y el vértice V. Es igual a p/2. Puntos interiores y exteriores: la parábola divide el plano en dos regiones. Los puntos que están en la región del foco se llaman puntos interiores (I), mientras que los otros son los exteriores (J). Cuerda: segmento que une dos puntos cualesquiera de la parábola. Cuerda focal: una cuerda que pasa por el foco F. Lado recto: Cuerda focal paralela a la directriz D y, por tanto, perpendicular al eje E. Su longitud es dos veces el parámetro (2p, pues se ven en la figura dos cuadrados unidos iguales de lado p).

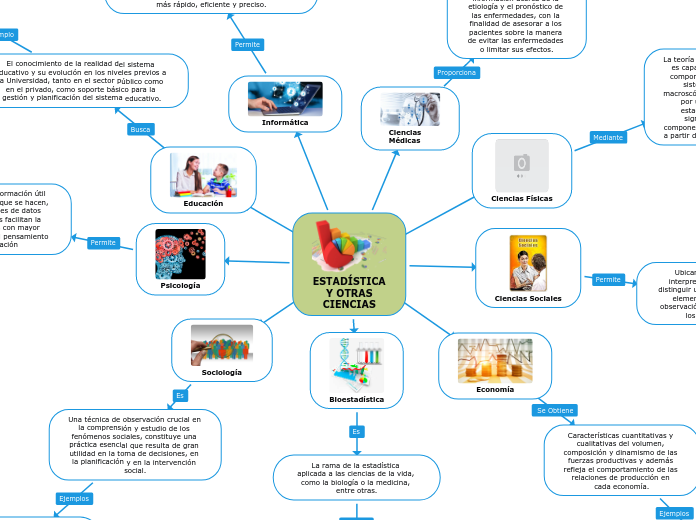
función exponencial y logarítmica

función logaritmica

Una función logarítmica es aquella que genéricamente se expresa como f (x) == logax, siendo a la base de esta función, que ha de ser positiva y distinta de 1. La función logarítmica es la inversa de la función exponencial

Propiedades de la función logarítmica Las propiedades generales de la función logarítmica se deducen a partir de las de su inversa, la función exponencial. Así, se tiene que: La función logarítmica sólo existe para valores de x positivos, sin incluir el cero. Por tanto, su dominio es el intervalo (0,+¥). Las imágenes obtenidas de la aplicación de una función logarítmica corresponden a cualquier elemento del conjunto de los números reales, luego el recorrido de esta función es R. En el punto x = 1, la función logarítmica se anula, ya que loga 1 = 0, en cualquier base. La función logarítmica de la base es siempre igual a 1. Finalmente, la función logarítmica es continua, y es creciente para a > 1 y decreciente para a < 1.

función exponencial

Se llama función exponencial de base a aquella cuya forma genérica es f (x) = ax, siendo a un número positivo distinto de Por su propia definición, toda función exponencial tiene por dominio de definición el conjunto de los números reales R. La función exponencial puede considerarse como la inversa de la función logarítmica

Propiedades de las funciones exponenciales Para toda función exponencial de la forma f(x) = ax, se cumplen las siguientes propiedades generales: La función aplicada al valor cero es siempre igual a 1: f (0) = a0 = 1. La función exponencial de 1 es siempre igual a la base: f (1) = a1 = a. La función exponencial de una suma de valores es igual al producto de la aplicación de dicha función aplicada a cada valor por separado. f (x + x?) = ax+x? = ax × ax? = f (x) × f (x?). La función exponencial de una resta es igual al cociente de su aplicación al minuendo dividida por la función del sustraendo: f (x - x?) = ax-x? = ax/ax? = f (x)/f (x?).

Se llama ecuación exponencial a aquella en la que la incógnita aparece como exponente. Un ejemplo de ecuación exponencial sería ax = b. Para resolver estas ecuaciones se suelen utilizar dos métodos alternativos: Igualación de la base: consiste en aplicar las propiedades de las potencias para lograr que en los dos miembros de la ecuación aparezca una misma base elevada a distintos exponentes: Ax = Ay. En tales condiciones, la resolución de la ecuación proseguiría a partir de la igualdad x = y. Cambio de variable: consiste en sustituir todas las potencias que figuran en la ecuación por potencias de una nueva variable, convirtiendo la ecuación original en otra más fácil de resolver. 22x - 3 × 2x - 4 = 0 t2 - 3t - 4 = 0

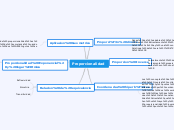
probabilidad

La probabilidad de un suceso es un número, comprendido entre 0 y 1, que indica las posibilidades que tiene de verificarse cuando se realiza un experimento aleatorio.

Probabilidad condicionada

independiente

Dos sucesos, A y B, son independientes cuando la probabilidad de que suceda A no se ve afectada porque haya sucedido o no B.

ejemplo: Al lazar dos dados los resultados son independientes.

p(A intersección B) = p(A) · p(B)

dependiente

Dos sucesos, A y B, son dependientes cuando la probabilidad de que suceda A se ve afectada porque haya sucedido o no B.

ejemplo: Extraer dos cartas de una baraja, sin reposición, son sucesos dependientes.

p(A intersección B) = p(A) · p(B/A)

sucesiones

Una sucesión es un conjunto de cosas (normalmente números) una detrás de otra, en un cierto orden.