MTE - Investigating Quantities
Decimals
Terminating Decimal Example:
2.5
Non-Terminating Decimal Example:
3.15259...
Repeating Non-Terminating Decimal Example:
3.333333...
Fractions
Iteration: counting fractional parts, the verbiage used to count fractions
Numerator: the top number in a fraction, the number that "counts"
Denominator: the bottom number in a fraction, represents what is being counted
Area Model: usually represented by separating pieces of a circle (as with a pie or pizza) or a rectangle (as with brownies or area, hence the name). This model includes two dimension, or a height and width, when representing fractional pieces
Linear Model: usually represented by splitting up lines, or one-deimensional areas (as with twizzlers, number lines, or one long rectangle)
Set Model: much like previous set models, this can be represented with specific objects (counters, blocks, shaded vs. not shaded circles, etc.) to show fractions of wholes affected (i.e., 1/2 could be represented by two counters, one shaded and one not)
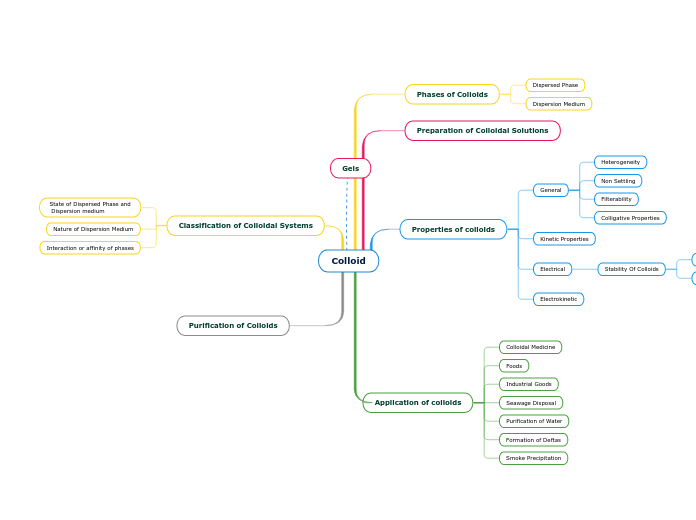
Integers
Concepts
Absolute Value: The distance a number is from zero. For example, the absolute value of -5 would be 5 because it is 5 units away from zero (or the origin)
Number Line Approach: This method focuses on magnitude and how far away an integer is from zero
Chip Method: This approach uses chips of either different colors or "open"/"closed" appearances to differentiate between positive and negative values. A set of one positive chip and one negative chip is called a "zero pair" and has a quantity of zero.
Operations
One example of using the chip method in addition...
-4+7=?
4 closed circles and 7 open circles represented would create 4 zero pairs leaving 3 open circles leftover. The answer is 3.
One example of using the chip method in subtraction...
-3-2=?
3 closed circles would be represented, but in order to take away 2 positives, we must add 2 zero pairs and cross out the two positive in the pairs. This leaves 5 total closed circles for an answer of -5.
***Using the takeaway method, zero pairs must be added on until you are able to take away the specified amount
Whole Numbers
Number Theory
*See Divvisbility Test Document in BB.
Prime #: A number with two different factors (one and itself). 1 is not a prime number.
Composite #: A number with more than two different factors. 0 has infinite factors but is not composite.
Strategies
Algorithms
Algorithms offer a sure way to solve problems and can typically be associated with the "standard" method of equation solving. Unlike strategies, there is only one algorithm and any other solid method is an alternate algorithm. (Standard vs. Expanded)
Properties
Examples of Properties-
Commutative Property:
3+2 = 6 = 2+3
Associative Property:
(3+2)+4 = 9 = 3+(2+4)
Distributive Property: (addition)
4(2+3) = (4x2)+(4x3) = 20
Identity Property:
7x1 = 7 = 1x7
etc...
Models
Addition Problem Types
Set Model: I have two robots and my roommate has five. How many do we have total?
Linear Model: I spent 10 minutes working on my mind map last Tuesday, and today I spent 35 minutes. How much total time have I spent on my mind map?
Subtraction Problem Types*
Takeaway Model: My roommate has seven robots and I took two of them for my collection. How many robots does my roommate have left?
Comparison Model: My roommate has four assignments due at midnight. I have eight. How many more assignments do I have than my roommate?
*excluding set and linear because those are included in addition
Numeration Systems
Types of Systems
Hindu-Arabic, Tally, Roman (Numerals), Egyptian, Mayan
***Our system is Hindu-Arabic, it is the most common and it is a DECIMAL system
***It is also a POSITIONAL system!
The attached video is a look into the Mayan system which is base-20 as opposed to our base-10.
Bases
Our system is based on tens, so we have a "base-10" system!
For example, each place value in our system represents a power of 10.
The first four place values are 100 , 101 , 102 , and 103