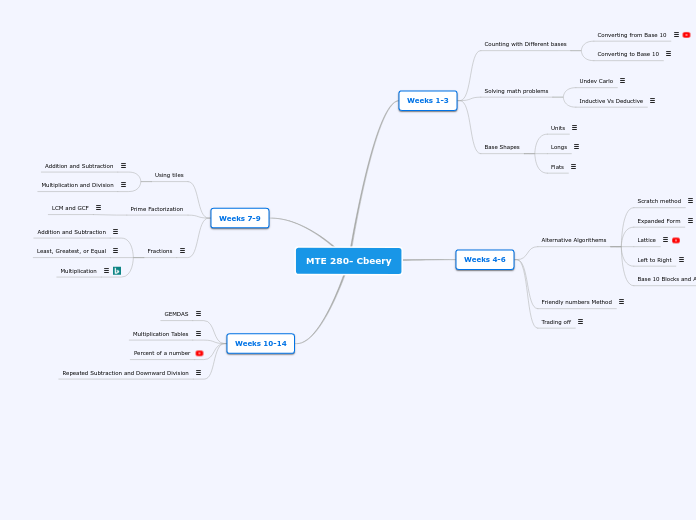
MTE 280- Cbeery
Weeks 10-14
Repeated Subtraction and Downward Division
Repeated Subtraction :
You subtract instead of grouping things together. You never have to carry. You subtract the number by the bigger number until you cannot anymore.
Upward Division:
Simplifying a fraction. So if you have 35/4 you see how many times 4 will go into 35 and solve from there.
Percent of a number
Multiplication Tables
2- If the last-digit is even
3- The sum of digits in number divided by 3
4- Last 2 digits in number divided by 4
5- Ends in a 5 or zero
6- If divisible by 2 and 3 then 6 will work
8- The last 3 digits in number divided by 8
9- The sum of digits in number divided by 9
10- Ends in a Zero
GEMDAS
Grouping
Exponents
Multiplication/Division
Addition/Subtraction
GEMDAS deals with groups so its better than PEMDAS because it makes more since (THAT'S WHY CASEY)
Weeks 7-9
Fractions
3/7
The 3 is how much you have
The 7 is the size of the whole piece
Multiplication
The easy way of solving for multiplying fractions is drawling it out.
Least, Greatest, or Equal
When the denominator is the same the bigger numerator is the greater number.
3/17 < 5/17
When the numerator is the same the denominator that's less is the greater number.
6/11 > 6/13
When the fraction has no similar part then you look at it like anchor fractions. You havee to figure out which piece has less of space that it has to take up.
13/14 < 16/17
Addition
1/4 + 3/8
1 (4) / 2x2 (4) + 3 (2) / 4x2 (2)
4/16 + 6/16 = 10/16
Use prime factors to solve for adding fractions.
For subtraction you do the same thing except for adding the fractions together you subtract.
Prime Factorization
LCM and GCF
LCM - Least Common Multiple, everything that they both have even if it isn't common
GCF - Greatest Common Factor, what they both have but the least exponent
28 2 I 36
2 x 14 2 I 18
2 x 7 3 I 9
3
Find one by multiplying prime factors. Start with 2 because that is the easiest prime number. For the other number use long division.
28 (2 x 2 x 7)
36 (2 x 2 x 3 x 3)
The LCM is 2squared x 3squared x 7
The GCF is 2squared
Using tiles
Multiplication and Division
-2(3)
This is the same thing as 0-2(3)
It says there are 2 groups of 3. However the zero just means you take away 2 groups of 3.
-2(3)
+++ +++ ++
_ _ _ _ _ _ _ _
The you take away 3 groups of the positive numbers so it equals to -6. You do this because it beings with a zero therefore there are zero pairs.
Addition and Subtraction
When adding and subtracting using tiles you look at the numbers you have and it tells you the negatives and the positives.
4 + (-5)
++++
_ _ _ _ _
You then see what you have in common and find the zero pairs . For this particular question the Answer is -1.
If it's negative you Keep Change Change
For bigger numbers that are being added and subtracted you only use one subtraction and addition sign.
-30+(-25)
_ (--)
If its both negative inside the parenthethes then you add the numbers together if they are opposite signs then it is subtrating the numbers
Weeks 4-6
Trading off
Trading off is..
24
+29
--------------
23
+30
--------------
Answer: 53
You trade only some of the numbers to the other number to make it a base 10 number
Friendly numbers Method
This method is where you set every number that you can do base 10 so that it is easier to add all up.
12+24+28+36+42
10+30+30+30+42
They both equal the same but its more friendly to add up the second one
Alternative Algorithems
Base 10 Blocks and Area Model
Base 10 blocks is when you draw all lines inside
Area Model is not drawing out all the lines and just making boxes
Left to Right
Addition
231
+432
--------
600
60
+ 3
-----
663
You literally add left to right instead of right to left
Multiplication
57
x 29
--------
4000
1000
140
1800
450
+ 63
_______
7,453
Lattice
Addition
232
+425
-------
(Draw a box then add downward)
001
+850
-------
851 (Answer)
Multiplication
43
x78
--------
Make a box then put the first number on top and the second number on the side (Watch Video)
Expanded Form
Addition
24+52=
20+4
50+2
Do this then add all of it together
Multiplication
24x45=
20+4
x 40+5
----------
800
1600
100
+ 20
------
2,520
Do this while multiplying
Scratch method
32
21
7
12
8
16
+22
---------
Count to ten the make a slash on the number and keep doing that until the bottom. The remainder of that goes on the bottom.
Weeks 1-3
Base Shapes
Flats
This is the biggest a set of 3 numbers can be after flats go back to units and keep going in sets of threes
It's usually the hundreds place
1_57
Longs
Longs are the bigger than units but smaller than flats
Usually in the tens place number
12_7
Units
Units are the first measurement and the smallest.
Usually in the ones digits place
125_
Solving math problems
Inductive Vs Deductive
Inductive: Finding a pattern
Deductive: Not in a pattern but in knowledge of the problem or concept
Undev Carlo
This means to understand the problem you are looking at
Step 2 would be to develop how you would solve the problem
Step 3 is how you are actually going to carry out the problem
The last step is to look over the answer and make sure it was done correctly.
Counting with Different bases
Converting to Base 10
You can solve this by multiplying how many times the number goes into each unit, long, and flat.
It consists of exponents and each number has its of exponent.
For example;
1525 would be 1^3+5^2+2^1+5^0
That being said the ones place is a zero exponent, tens place is a one exponent, hundreds place is a two exponent, thousands is a three exponent, and so on.
If the Base is 5 and the Number is 1525 then it would be solved looking like this.
1(5^3)+5(5^2)+2(5^1)+5(5^0)
Without a calculator you would multiply the 5 by itself as many times as the number of the exponent
For Example;
5^2 would be 25
5^3 would be 125 multiplying 5*5*5
Converting from Base 10
This can be solved by downward division with the base number being the number we will divide from.
If the base is 5 and the base 10 number is 1525 then it would look like this:
5|_1525__
Then solve how 5 would go into 1525.