MTE Investigating Quantity
Rational Numbers
Fractions
Addition and Subtraction:
Adding or subtracting fractions are easier to do when you use the area, linear, or set models. When you solve fraction operations with common denominators, you can just keep adding parts until you find your answer. With uncommon denominators, it gets harder. You have to use the equivalent fraction methods to figure out a common denominator to add in parts. If you go over a whole and into a mixed number with either common or uncommon denominators, you can still use the same models, you just have to find the common denominator, and multiply the numerator with the same number, and then change your models to match.
Different Models for fractions:
Three models: Area Model, Linear Model, and Set Model.
Area model deals with one large object. Linear allows you to use a number line to illustrate fractions, or a smaller skinnier object into pieces. Set model deals with individual objects that cannot be broken into or "sliced"
Mixed numbers is when you have at least one whole and more parts of a whole. For example 2 3/4 is 2 wholes and 3 parts of a whole that has been divided into 4.
Decimals
Used Base 10 blocks to represent the different decimals.
Cubes= tens
flats= ones
longs=tenths
units=hundredths
Integars
Integer Operations
Integer Concepts
An integer is the opposite of counting numbers, counting numbers and zero. If you look at it from a number line point of view, the integer and the opposite of it are the same distance from 0 on a number line.
Whole Number Operations
Number Theory
Strategies
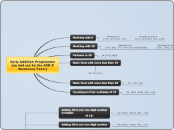
Addition and subtraction strategies
1. Compensating-
58+33
(+2) 60+33=93-2=91
68-33
(-8) 60-33=27+8=35
2. Decomposing-
*harder to write out instead of draw than I assumed
Algorithms
An algorithm is different from a strategy because an algorithm is going to be the same steps and roles every time in the math problem, but a strategy is process that changes depending on the numbers and how you approach the problem.
1. Traditional Algorithm
68 68
+33 -33
101 35
- Alternate Algorithms
2. Partial Sum-
630 + 155
630
+ 155
700
80
5
785
Fact Families
Fact Families are three related numbers. To understand how to do fact families you must understand the communicative property of multiplication AND addition and inverse relationships.
Example of a fact family:
5+7+12
7+5=12
12-5=7
12-7=5
Properties
Properties:
Addition
1. Closure Property of Addition
-If you add any two whole numbers together, their sum will be a whole number
2. Commutative Property of Addition
-Changing the order of addends will result in the same sum
3. Associative Property of Addition
-When adding 3 or more numbers, changing the order of the grouping will result in the same sum
4. Identity Property of Addition
-When adding zero to any number, the sum will remain the same
-Must work both ways of problem
Subtraction
1.None of the properties apply to subtraction
Multiplication
1. Closure Property of Multiplication
2. Commutative Property of Multiplication
3. Associative Property of Multiplication
4. Identity Property of Multiplication
5. Zero Property of Multiplication
6. Distributive Property of Multiplication over Addition for whole numbers
Problem Types
Addition
Set Model- Characterized by the combining of two sets of separate objects
Linear Number line- Characterized by the combining of two continuous quantities (measured by time & distance)
Subtraction
Take Away- Starting with some given quantity and taking away a specific amount from said quantity
Missing Addend- Determine what quantity needs to be added to reach the sum, this model is closely related to subtraction and addition because it uses related addition facts to find the missing addend in a subtraction problem
Comparison- Comparing two quantities to find out how much larger or smaller one is than the other
Linear- Used on a number line to show change, usually with continuous quantities
Multiplication
Multiplication
Repeated Addition (Set)- repeatedly adding a quantity of objects aspecified number of times (discrete)
Repeated Addition (Linear/Number Line Model)- repeatedly adding a quantity of continuous quantities a specified number of times.
Area Model- product of two numbers representing the sides of a rectangular region,such that the product represents the numbers of unit size squares within that region which equals the area
Numeration Systems
Place Value
Bases
Base 10- Has ten digits: 0,1,2,3,4,5,6,78,9. The Hindu Arabic system is this base.
Base 5: has five digits: 0,1,2,3,4. Base five is based on fingers, so one hand counts 0,1,2,3,4 and 10 for one hand. Then, 11,12,13,14 and 20 for two hands. So 31 would be represented as three hands and one finger or 31 base five.
Base 2: has two digits: 0 and 1. One counts like 0,1 then 10, 11, 100, 101, 110, 111, 1000, where 1000 would be eight in a base ten system.
Different Systems
Tally- use tally's to represent every (1) thing counted. To group together tallies, you put one diagonal line across for straight tallies to signal "5."
Hindu Arabic- system has 10 digits, 0,1,2,3,4,5,6,7,8,9 and 10, and place value is on powers of ten, used in the United States. Also known as "base 10"
Roman Numerals- a European system. An example, V is 5. So IV would be 4 (5-1), and CM equals 900 (1000-100).
Here is a website further explaining roman numerals:
https://www.mathsisfun.com/roman-numerals.html