par Cristiana Pandolfi Il y a 1 année
123
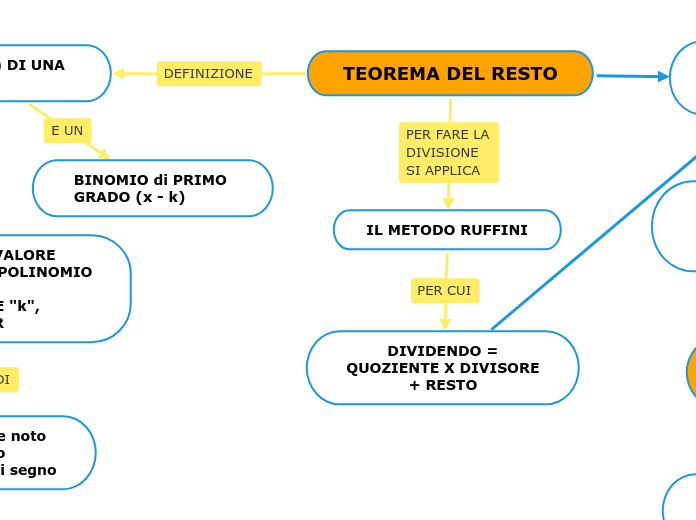
TEOREMA DEL RESTO
Il teorema del resto afferma che il resto di una divisione di un polinomio per un binomio di primo grado è uguale al valore che il polinomio assume quando la variabile 'x' viene sostituita con il termine noto del binomio cambiato di segno.
