Una medida comparativa en didáctica de las matemáticas
entre el análisis a priori y la contingencia
3 Formalización de la comparación entre el análisis a priori y el análisis
de la contingencia
3.3 Construcción de un test de hipótesis de adecuación a priori-a
posteriori
3.2 Construcción de una medida comparativa
3.1 Retorno al ASI
2 Problemática
El análisis a priori permite evidenciar relaciones de similitud y relaciones
implicativas a priori entre las variables. Estas relaciones son, por supuesto,
hipotéticas y basadas sobre el conocimiento de los aprendizajes conocidos o
supuestos conocidos y de las condiciones de enseñanza. Aquí, nos interesamos
esencialmente en las relaciones implicativas, del conocimiento de las reglas, según
el vocabulario del “Data mining”. Se trata entonces de comparar las calidades
implicativas de las relaciones del tipo ⇒ ba obtenidas por el análisis a priori, por
ejemplo, por las concepciones de los alumnos ficticios, y aquellas conseguidas por
el análisis a posteriori, que preferimos llamar análisis de la contingencia, porque se
apoya directamente sobre la base de los comportamientos observados en una
prueba
1 Datos
Los datos de una investigación en un contexto de prueba de evaluación de una
lección, generalmente, están compuestos de los siguientes elementos:
- un conjunto de ítems o variables V en número v,
- un conjuntos de sujetos Y en número n,
- un conjunto W de actitudes, concepciones, comportamientos
generales esperados en el curso de la p
Regla y R-regla de excepción en Análisis Estadístico
Implicativo
4 Relación entre las intensidades de implicación de a ∧ b sobre c y sobre
no c
Subtopic
4.1. Modelo binomial
4.1 Modelo de Poisson
3 Interpretación e ilustración de las reglas de excepción
3.2 Ejemplo numérico
3.1 Dos enfoques para la caracterización de las reglas de excepción
2 Principios del ASI – Repaso
Denotemos A y B los subconjuntos respectivos de E de individuos que
verifican respectivamente las variables a y b. Para una regla cualquiera a→ b,
observada en E, el ASI consiste en comparar el número de contraejemplos ba n ∧ a
dicha regla observados en A ∩ B , con el número de contraejemplos que aparecen
en una extracción aleatoria e independiente de dos partes X e Y de E con los
mismos cardinales respectivos que A y B (Figura 1) (cf. (Gras, 2005) y (Lebart et
al., 2006)). La variable aleatoria asociada se denota ba N
Descubriendo Reglas de Excepción Estructuradas
5 Esquema de evaluación para descubrir Reglas/Grupos de excepción
Actualmente los artículos que proponen un método para descubrir
reglas/grupo de excepción, típicamente evalúan su método por una disminución del
número de reglas descubiertas o un éxito en un estudio de caso. Una disminución
del número de reglas descubiertas representa un criterio cuantitativo importante
que típicamente produce una reducción de los costos de inspección para salidas de
minería de datos. Sin embargo, este criterio de evaluación tiene una deficiencia
seria, que es que descuida la importancia de las reglas descubiertas.
4 Evaluación experimental
4.4 Evaluación del estudio de Meta patrones para la Representación del
Conocimiento
4.3 Efectividad del Umbral Fijo para PADRE
4.2 Efectividad de PADRE
3 Métodos para el Descubrimiento de Pares de Reglasc
3.4 Estudio de Meta patrones para la Representación del Conocimiento
3.3 Fijación de umbrales para PADRE
3.2 PADRE con su Evaluación de Fiabilidad Simultánea
3.1 MEPRO con su medida de interés
2 Descripción del Problema
Asumimos que un ejemplo i e es una descripción de un objeto incluido en un
conjunto de datos en forma de un registro y ese conjunto de datos contiene n
ejemplos ne,..., 2e, 1
e . Un ejemplo i e está representado por una m-upla
imii ,...,, yyy 21 donde imii ,...,, yyy 21 son valores de m atributos discretos. Aquí se
supone que un atributo continuo ha sido convertido en un atributo nominal usando
un método existente, como se muestra en (Dougherty et al., 1995). Un evento
representando el valor asignado a un atributo será llamado átomo
Conceptos fundamentales del Análisis Estadístico Implicativo
(ASI) y su soporte computacional CHIC
Tipicalidad y contribución
Variable más típica o más contributiva, y también qué otras categorías pueden
conducir a los mismos valores de tipicalidad y/o contribución.
La noción de tipicalidad se define por el hecho de que ciertos individuos son
“típicos” del comportamiento de la población, es decir con una intensidad de
implicación similar a la de la regla. La noción de contribución se define para
determinar los individuos que contribuyen bien a la creación de la regla. Estos
individuos son más responsables que otros de la formación de la regla.
Tipicalidad y contribución de individuos en el Análisis implicativo
Tipicalidad y contribución de individuos en el Análisis clasificatorio
4 Análisis cohesitivo
La cohesión surge como una medida de la calidad implicativa de la R-regla.
El objetivo es descubrir R-reglas ´´´ → RR con una fuerte relación implicativa
entre las componente de ´ R y las de ´´ R . Por ejemplo, es natural formar la regla
( ) ( ) 21 43 →→→ aaaa si las relaciones implicativas 31 → aa , 41 → aa ,
32 → aa y 42 → aa son lo suficientemente significativas
3 Análisis Estadístico Implicativo
La Intensidad de la implicación entre variables
En la jerarquía dirigida, el árbol que se forma no está necesariamente
conectado, lo cual significa que esta jerarquía sólo contiene clases importantes de
acuerdo a la medida de calidad adoptada.
Los nodos internos del árbol dirigido, los cuales representan la jerarquía
dirigida, describen relaciones implicativas complejas, llamadas R-reglas, entre los
atributos de A.
2 Análisis Clasificatorio
Ya que su objetivo es agrupar objetos similares, se necesita alguna medida
para evaluar las diferencias y similitudes entre objetos. El concepto de similaridad
es fundamental. La similaridad es una medida de correspondencia o semejanza
entre los objetos que van a ser agrupados
2.2 Nodos significativos
2.1 Árbol de Similaridad
Datos
Para ejemplificar los cálculos que deben realizarse, tanto en el Análisis
Clasificatorio como en el Análisis Estadístico Implicativo, que veremos más
adelante, utilizaremos los datos de la investigación desarrollada por Pitarch en el
2002, en la cual se analizó el razonamiento de los alumnos de la Enseñanza
Secundaria Obligatoria (ESO), utilizando simultáneamente el tratamiento
El sistema informático CHIC
El sistema informático CHIC (Classification Hiérarchique Implicative et
Cohésitive) es un software de análisis de datos, inicialmente concebido por Regis
Gras con relación a las técnicas del Análisis Estadístico Implicativo, el cual ha sido
sucesivamente desarrollado para las computadoras personales por Saddo Ag
Almouloud, Harrisson Ratsimba-Rajohn y, en su versión actual, por Raphaël
Couturier (Versión 4.1).
CHIC: utilización y funcionalidades
6 Ilustración con las variables sobre intervalo y el cálculo de las
tipicalidades y de las contribuciones
5 Otras posibilidades
4 Grafo implicativo
3 Árbol de similaridad y árbol jerárquico
2 Variables
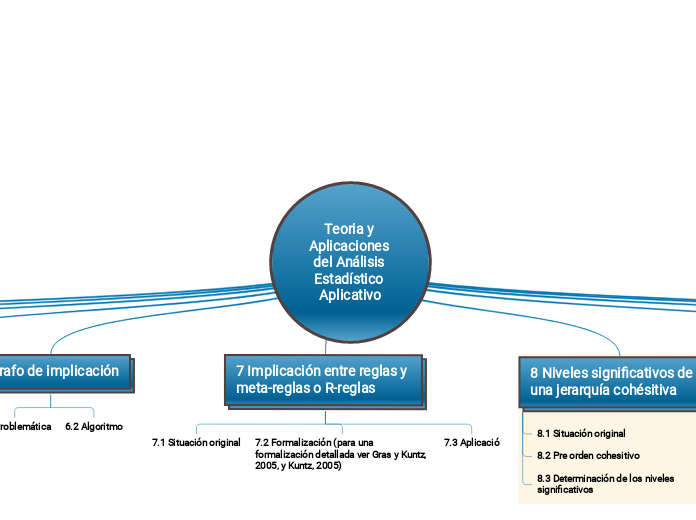
Teoria y Aplicaciones del Análisis Estadístico Aplicativo
This mind map comes in handy if you are in the middle of job searching. Gather all the possibilities, then with the help of the mind map choose whichever fits your needs best.
Topic principal
9 Tipicalidad y contribución de los sujetos y de las variables
suplementarias
9.5 Aplicación
9.4 Tipicalidad y contribución de un sujeto y de una variable
suplementaria a una clase o un camino
9.4.2 Contribución
9.4.1 Tipicalidad
9.1 Situación fundamental
9.2 Potencia implicativa de una clase y de un camino
9.3 Potencia implicativa de un sujeto sobre una clase o un camino y
distancia a esta clase o camino
8 Niveles significativos de una jerarquía cohésitiva
8.3 Determinación de los niveles significativos
8.2 Pre orden cohesitivo
8.1 Situación original
Keep track of your applications so you won't send it twice to the same employer.
You can also separate the responses which might turn into an offer.
7 Implicación entre reglas y meta-reglas o R-reglas
7.3 Aplicació
7.2 Formalización (para una formalización detallada ver Gras y Kuntz,
2005, y Kuntz, 2005)
7.1 Situación original
6 Grafo de implicación
6.2 Algoritmo
6.1 Problemática
5 La implicación-inclusión
5.3 El índice de implicación-inclusión
List here the people you have been in contact with, in case you would need to follow up with them later on.
la calidad inductiva, es el número:
( ) ( )( ) [ ] 21
ϕ⋅=ψ b,ab,aib,a
que integra a la vez el asombro estadístico y la calidad inclusiva.
5.2 Un índice de inclusión
Add your appointments here!
La solución9
que aportamos utiliza a la vez la intensidad de implicación y otro
índice que da cuenta de la disimetría entre las situaciones 1 = )bya(S y
1 )bnoya(S' = , (respectivamente 2 = )bnoyano(S y 2 )bnoya(S' = en virtud de
la primera nombrada. La debilidad relativa de las instancias que contradicen la
regla y su contrapuesta es también fundamental.
5.1 Situación original y problemática
Use our mind map to prepare for an interview and prepare individually for each company that called you for an interview.
- Cuando el tamaño de las muestras tratadas, y en particular el de E, crece (del
orden del millar y más), la intensidad ϕ b)(a, tiende a no discriminar
suficientemente ya que sus valores pueden ser muy próximos a 1, mientras que
la inclusión cuya calidad se busca o pretende modelar, dista mucho de ser
satisfecha (fenómeno indicado en (Botín A., 1997) que trata de la
4 Caso de las variables-sobre-intervalos y variables-intervalo
You might get offers at first or you might need to negotiate; either way, list here all of your offers so you can easily compare them and choose.
4.2 Variables-intervalos
4.2.1 Situación original
4.2.2 Algoritmo
tomados según los sujetos para las variables a y b son de naturaleza simbólica,
con frecuencia en los intervalos de + R , es posible extender los algoritmos
anteriores [Gras R. 17 c, 2001]. Por ejemplo, a la variable a se le asocian los
intervalos de peso y a la variable b los intervalos de estatura, intervalos debidos a
una imprecisión de las medidas. Efectuando la unión de los intervalos xI y x J
descritos por los sujetos x de E , según cada una de las variables a y b
respectivamente, se obtienen dos intervalos I y J que cubren todos los valores
posibles de a y b . Sobre cada uno ellos se pueden definir una partición en un
determinado número de intervalos que respetan, como se explicó anteriormente, un
determinado criterio de optimalidads
Se dispone de los datos proporcionados por una población de n individuos
(que pueden ser cada uno ciertos conjuntos de individuos, por ej. una clase de
alumnos) según p variables (por ej. notas sobre un año en francés, matemáticas,
física…, pero también podría ser: peso, estatura, ancho de pecho…). Los valores
tomados por estas variables según cada individuo son intervalos de números reales
positivos. Por ejemplo, el individuo x refleja el valor [12; 15,50] en la variable nota
de matemáticas. E. Diday hablaría de este sujeto de p variables simbólicas en
términos de valores intervalos definidos sobre la población
4.1 Variables- sobre-intervalo
4.1.1 Situación original
4.1.2 Primer problema
4.1.3 Segundo problema
Se supone ahora que los intervalos [ ] 21 a,a y [ ] b,b 21 se proveen de
particiones optimales P y Q, respectivamente, en el sentido de las nubes dinámicas.
Sean p y q los números respectivos de subintervalos que componen P y Q. A
Nos vamos a interesar por el intervalo [ ] 21 a,a , suponiéndolo provisto de una
partición inicial trivial de subintervalos de igual longitud, pero no necesariamente
de igual distribución de frecuencias observadas sobre estos subintervalos.
Denotemos por = { } A,...,A,AP P002010 , esta partición en p subintervalos. Se
pretende obtener una partición de [ ] 21 a,a en p subintervalos A,...,A,A qP2q1q de tal
forma que en cada subintervalo se tenga una buena homogeneidad estadística
(escasa varianza intra-clase) y que estos subintervalos presentan una buena
heterogeneidad mutua (fuerte inercia inter-clase).
Se busca, por ejemplo, extraer de un conjunto de datos biométricos la regla
siguiente, considerando su calidad: “si un individuo pesa entre 65 y 70kg entonces
en general mide entre 1.70 y 1.76m “. Una situación comparable se presenta en la
investigación de la relación entre intervalos de resultados de alumnos en dos
disciplinas diferentes. La situación más general se expresa entonces así: dos
variables reales a y b toman una serie de valores sobre 2 intervalos finitos [ ] 21 a,a y
[ ] b,b 21 . Sea A (resp. B) el conjunto de los valores de a (resp. b) observados sobre
[ ] 21 a,a (resp. [ ] b,b 21 )
3 Casos de variables modales y frecuenciale
3.2 Formalización
Esta solución aportada al caso modal es también aplicable al caso de las
variables frecuenciales, o incluso al de las variables numéricas positivas, bajo la
condición de haber normalizado los valores observados sobre las variables, tales
como a y b, la normalización en [0,1] es hecha a partir del máximo del valor
tomado respectivamente por a y b sobre el conjunto E.
3.1 Situación original
Gather here all the documents you have prepared, the cover letters, recommendations, resumes, etc.
Con el fin de ponerlo en evidencia, se les proponen algunas palabras significativas
que deben jerarquizar. Sus elecciones ya no son binarias, las palabras elegidas por
un profesor cualquiera son ordenadas de menor a mayor representatividad. La
interrogación de M. Bailleul se centra entonces en cuestiones del tipo: “si yo elegí
tal palabra con tal importancia, entonces yo elijo otra palabra con una importancia
al menos igual”. Entonces fue necesario extender el concepto de implicación
estadística a otras variables no binarias. Este es el caso de las variables modales
que son asociadas a fenómenos donde los valores (xa ) son números del intervalo
[ ]1,0 y que describen grados de pertenencia o satisfacción como es en el caso de la
lógica difusa
2 La intensidad de implicación en el caso binario
2.4 Estabilidad del índice de implicación
Estudiar la estabilidad de q, equivale a examinar sus pequeñas variaciones en
una vecindad de los 4 valores enteros observados ( ) ba ba nyn,n,n ∧ . Para ello, es
posible efectuar distintas simulaciones cruzando las 4 variables enteras de las que q
depende ((Fleury, 1996) o (Gras et al, 2004a)). Pero, consideremos estas variables
como números reales y a q como una función continuamente diferenciable con
relación a las mismas, obligadas a respetar las desigualdades: na , nb y
[ ] ∧ba ≤ n,ninfn ba y [ ] ba ≤ nn,nsup .
2.3 Formalización
Para formalizar esta cuasi-regla, consideremos, como hizo I. C. Lerman para
la similaridad, dos partes cualesquiera X e Y de E, elegidas aleatoria e
independientemente (ausencia de vínculo a priori entre estas dos partes) y de
cardinales iguales a los de A y B respectivamente. Sean Y y B los complementos
respectivos de Y y de B en E de igual cardinal b b = − nnn .
2.2 Matematización
Dado un conjunto finito V de v variables: a, b, c… En la
situación paradigmática clásica, se trata de los resultados (éxito-fracaso) a un ítem
de un cuestionario. A un conjunto finito E de n sujetos x, se asocian, por abuso de
escritura, las funciones del tipo: → (xax ) donde ( ) = 1xa (o (xa ) = verdadero ) si x
satisface o posee el carácter a y 0 (o ( ) = falsoxa ) en caso contrario. En inteligencia
artificial se dirá que x es un ejemplo o una instancia para a si ( ) = 1xa y un
contraejemplo en el caso contrario
2.1 Situación fundamental y original
Type in here your dream job, or the next best thing you would do for a living.
You can also write down those companies who you would gladly work for.
Se interrelaciona una población E de objetos o sujetos con variables
(caracteres, criterios, éxitos…) formulándose la siguiente pregunta: ¿"en qué
medida se puede considerar que de cumplirse la variable2
a implica que se cumpla
la variable b? Dicho de otra forma, ¿los sujetos tienen la tendencia a ser b si se
sabe que son a?". En las situaciones naturales, humanas o de las ciencias de la
vida, donde los teoremas (si a entonces b) en sentido deductivo del término no
pueden establecerse a causa de las excepciones que los niegan, es importante para
el investigador y el experto "profundizar en sus datos" con el fin de lograr reglas
suficientemente fiables (de las clases de "teoremas parciales", de las inducciones)
para poder conjeturar3
una posible relación causal, una génesis, para describir,
estructurar una población y hacer la hipótesis de una determinada estabilidad con
fines descriptivos y, si es posible, predictivos