Стежками
многогранників
та тіл
обертання
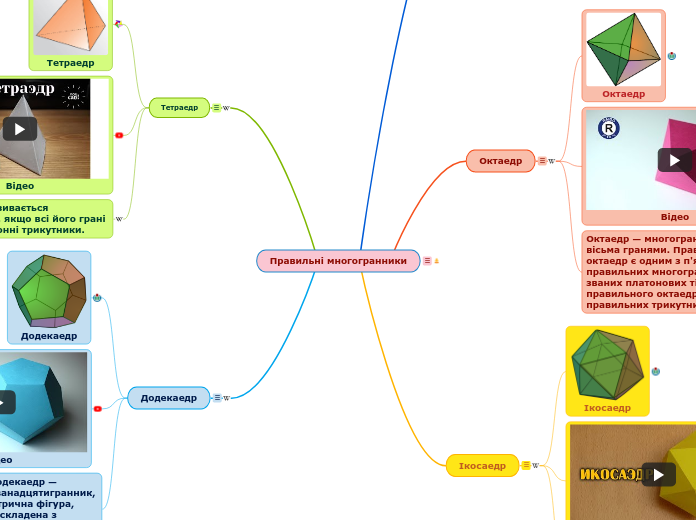
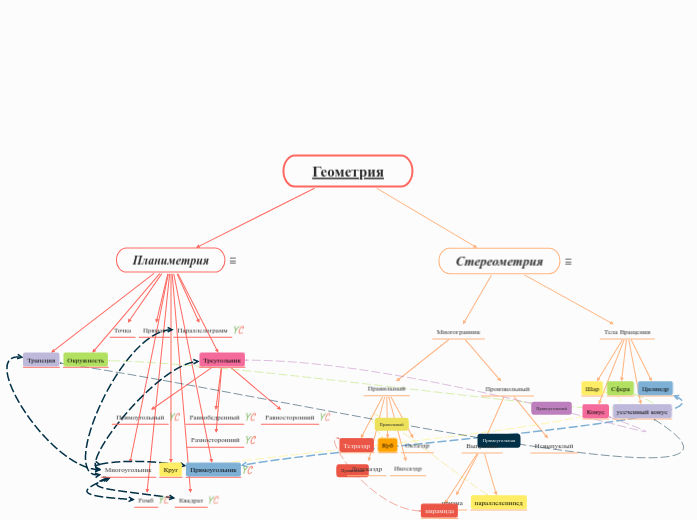
Многогранник — це геометричне тіло, поверхня якого складається із скінченого числа плоских многокутників.
Гранями многогранника називаються частини площин (многокутники), які обмежують многогранник.
Ребрами многогранника називаються спільні сторони суміжних граней (многокутників).
Вершинами многогранника називаються вершини многогранних кутів, утворених його гранями, що сходяться в одній точці.
Діагоналлю многогранника називається відрізок прямої, яка сполучає дві вершини многогранника, що не лежать в одній грані.
Діагональною площиною многогранника називається площина, що проходить через три вершини многогранника, які не лежать в одній грані.
Перерізом многогранника площиною називається частина цієї площини, яка обмежена лінією перетину поверхні многогранника з цією площиною.
Многогранник називається опуклим, якщо він цілком лежить по одну сторону від площини будь-якої його грані. Гранями опуклого многогранника можуть бути тільки опуклі многокутники.
Сфера
Сферою називається поверхня, яка складається з усіх точок простору, що знаходяться на даній відстані (яка називається радіусом) від даної точки (яка називається центром). Відрізок, який з’єднує дві точки сфери і проходить через її центр називають діаметром сфери.
Конус
Конус — тіло обертання, яке виходить в результаті обертання прямокутного трикутника навколо його катета.
Розгорткою бічної поверхні конуса є круговий сектор. Довжина дуги сектора — це довжина кола основи конуса довжиною 2πR , кут розгортки бічної поверхні α .
В конусі не можна позначити кут розгортки. На розгортці конуса не можна позначити висоту і радіус конуса.
Радіус сектора — це твірна конуса.
Зрізаний конус
Циліндр
Циліндр — це тіло обертання, яке виходить при обертанні прямокутника навколо його сторони.
Осьовий переріз циліндра — це перетин циліндра площиною, яка проходить через вісь циліндра. Цей переріз є прямокутником.
При перерізі циліндра площиною, паралельною осі циліндра (тобто перпендикулярною основі), також виходить прямокутник.
Переріз циліндра
Комбінації тіл
Многогранник називається вписаним у кулю, якщо всі його вершини лежать на поверхні кулі.
Многогранник називається описаним навколо кулі, якщо всі його грані дотикаються поверхні кулі.
Якщо кола двох основ циліндра лежать на деякій сфері, то кажуть, що циліндр вписано в сферу або що сфера описана навколо циліндра. Вважають, що сфера вписана в циліндр, якщо вона дотикається його основ, а з бічною поверхнею має одне спільне коло. Не в кожний циліндр можна вписати коло.
Якщо вершина конуса і коло його основи лежать на деякій сфері, то кажуть, що конус вписано в сферу, а сфера описана навколо конуса.
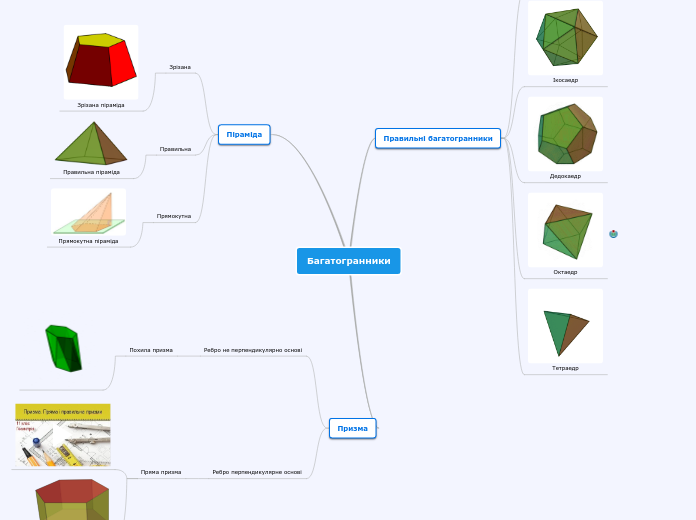
Піраміди
Багатогранник, одна грань якого є n — кутником, а інші грані — трикутники із загальною вершиною, називається пірамідою, n -кутник називається основою піраміди, а трикутники — бічними гранями.
Спільна вершина бічних граней називається вершиною піраміди.
Відрізки, що з'єднують вершину піраміди з вершинами основи, називаються ребрами піраміди.
Залежно від кількості сторін основи, піраміди можуть бути трикутними, чотирикутними, п'ятикутними і т. д.
Призми
Призма — це многогранник, дві грані якого є рівними многокутниками, що знаходяться в паралельних площинах, а інші грані — паралелограми.
Грані, які знаходяться в паралельних площинах, називаються основами призми, а інші грані — бічними гранями призми.
Призма, бічні ребра якої не перпендикулярні основам, називається похилою призмою.
Похила
призма
Пряма призма
Куля
Кулею називається тіло, утворене з усіх точок простору, що знаходяться на відстані, не більшій за дану (яка називається радіусом) від даної точки (яка називається центром). Кулю можна отримати в результаті обертання круга навколо його діаметра.
Будь-який переріз кулі площиною є круг, а переріз сфери площиною є коло.