Чотирикутники

Még több ilyen

Стежками многогранників

Szerző: Дар'я Бевз

Площа паралелограма, трикутника

Szerző: Daniil Martenenko

Площі фігур

Szerző: Анастасия Поливода

Многокутники

Szerző: Татьяна Сенникова

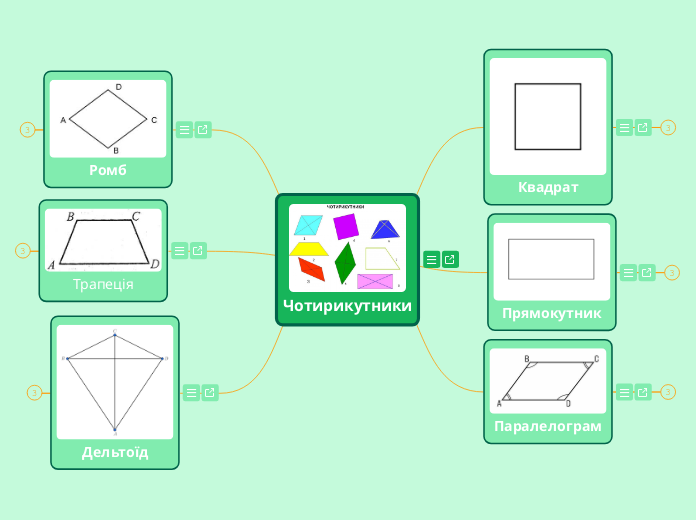
Чотирикутники

Чотирикутник — це частина площини, обмежена простою замкненою ламаною, яка містить чотири (4) ланки. Вона складається з чотирьох (4) вершин і чотирьох сторін , що послідовно їх сполучають. При цьому жодні три з даних точок не повинні лежати на одній прямій. Вершини чотирикутника називаються сусідніми, якщо вони є кінцями однієї з його сторін. Несусідні вершини називаються протилежними. Відрізки, що сполучають протилежні вершини чотирикутника, називаються діагоналями.

Дельтоїд

• Неправильний чотирикутник: не має паралельних сторін.

Периметр дельтоїда

Периметр дельтоїда :

Площа дельтоїда

Площа, що обмежується дельтоїдою, S = 2 9 π R 2

Діагональ дельтоїда

Одна діагональ ділить дельтоподібний м'яз на два рівних трикутника. Інша діагональ ділить дельтоподібний м'яз на два рівнобедрених трикутника, якщо він опуклий, і завершує його рівнобедреним трикутником, якщо він не опуклий.

Трапеція

• Трапеція: одна пара протилежних сторін є паралельною.

Периметр трапеції

Формула визначення периметра трапеції:

1. Формула периметра через основи:

P = a + b + c + d

Площа трапеції

Формули визначення площі трапеції:

1. Формула площі через основи та висоту:S = (a + b)· h2

2. Формула площі через середню лінію та висоту:

S = m · h

3. Формула площі через діагоналі та кут між ними:S = d₁d₂· sin γ = d₁d₂· sin δ22

4. Формула площі через чотири сторони:S = a + b√c² -((a - b)² + c² - d ²)²22(a - b)

5. Формула Герона для трапеції:S = a + b√(p - a)(p - b)(p - a - c)(p - a - d)|a - b|деp = a + b + c + d  - півпериметр трапеції.2

Діагоналі трапеції

Формули визначення довжин діагоналей трапеції:

1. Формули діагоналей за теоремою косинусів:

d₁ = √a² + d² - 2ad·cos β

d₂ = √a² + c² - 2ac·cos α

Ромб

• Ромб: всі чотири сторони мають однакову довжину. Або еквівалентно: діагоналі перпендикулярні і перетином ділять навпіл одна одну. Не формально це є «сплюснутий квадрат» (але строго математично квадрат теж є ромбом).

Площа ромба

Площа ромба - це простір, обмежений сторонами ромба, тобто в межах периметра ромба.

Формули визначення площі ромба:

1. Формула площі ромба через сторону і висоту:

S = a · h_a

Периметр ромба

Периметром ромба називається сума довжин всіх сторін ромба.

Довжину сторони ромба можна знайти за формулами, вказаними вище.

Формула визначення довжини периметра ромба:

Формула периметра ромба через сторону ромба:

P = 4a

Діагоналі ромба

Діагональ ромба - це довільний відрізок, що з'єднує дві вершини протилежних кутів ромба.

Ромб має дві діагоналі - більшу d₁, та меншу - d₂

Формули визначення довжини діагоналі ромба:

1. Формули більшої діагоналі ромба через сторону і косинус гострого кута (cosα) або косинус тупого кута (cosβ)

d₁ = a√2 + 2 · cosα

d₁ = a√2 - 2 · cosβ

Паралелограм

• Паралелограм: чотирикутник із двома парами паралельних сторін. еквівалентною умовою є те, що його протилежні сторони мають однакову довжину; що протилежні кути рівні; або що діагоналі перетинаються і ділять одна одну навпіл. До паралелограмів відноситься ромб, прямокутник, а також квадрат.

Площа паралелограма

Площею паралелограма називається простір який обмежений сторонами паралелограма, тобто в межах периметру паралелограма.

Формули визначення площі паралелограма:

1. Формула площі паралелограма через сторону та висоту, проведену до цієї сторони:

S = a · h_a

S = b · h_b

Периметр паралелограма

Периметром паралелограма називається сума довжин всіх сторін паралелограма.

Формули визначення довжини периметру паралелограма:

1. Формула периметру паралелограма через сторони паралелограма:

P = 2a + 2b = 2(a + b)

Діагоналі паралелограма

Діагоналлю паралелограма називається будь-який відрізок який сполучає дві вершини протилежних кутів паралелограма.

Паралелограм має дві діагоналі - довшу, нехай будеd₁, та коротшу - d₂

Формули визначення довжини діагоналі паралелограма:

1. Формули діагоналей паралелограма через сторони та косинус кута β (за теоремрю косинусів)

d₁ = √a² + b² - 2ab·cosβ

d₂ = √a² + b² + 2ab·cosβ

Прямокутник

• Прямокутник: всі чотири кути є прямими кутами. Еквівалентно: діагоналі мають однакову довжину і при перетині діляться навпіл. До прямокутників відноситься і квадрат.

Площа прямокутника

Площею прямокутника називається простір який обмежений сторонами прямокутника, тобто в межах периметру прямокутника.

Формули визначення площі прямокутника

1. Формула площі прямокутника через дві сторони:

S = a · b

Периметр прямокутника

Периметром прямокутника називається сума довжин всіх сторін прямокутника.

Формули визначення довжини периметру прямокутника

1. Формула периметру прямокутника через дві сторони прямокутника:

P = 2a + 2b

P = 2(a + b)

Діагональ прямокутника

Діагоналлю прямокутника називається будь-який відрізок, який сполучає дві вершини протилежних кутів прямокутника.

Формули визначення довжини діагоналі прямокутника

1. Формула діагоналі прямокутника через дві сторони прямокутника (через теорему Піфагора):

d = √a² + b²

Квадрат

• Квадрат (правильний прямокутник): всі чотири сторони мають однакову довжину, а чотири кути є прямими. Діагоналі перетинають одна одну навпіл і під прямим кутом, а також мають однакову довжину. Чотирикутник є квадратом тоді і лише тоді, коли він одночасно є ромбом і прямокутником (чотири рівні сторони і чотири однакові кути).

Площа квадрата

Площею квадрата називається простір який обмежений сторонами квадрата, тобто в межах периметру квадрата.

Площа квадрата більша площі будь-якого чотирикутника з таким же периметром.

Формули площі квадрата:

1. формула площі квадрата через сторону квадрата:

S = a²

Периметр квадрата

Периметром квадрата називається сума довжин всіх сторін квадрату.

Формули визначення довжини периметра квадрата:

1. Формула периметра квадрата через сторону квадрата:

P = 4a

Діагональ квадрата

Діагоналлю квадрата називається будь-який відрізок, який сполучає дві вершини протилежних кутів квадрата.

Діагональ будь-якого квадрату завжди більша за його сторону в √2 раз.

Формули визначення довжини діагоналі квадрата:

1. формула діагоналі квадрата через сторону квадрата:

d = a·√2