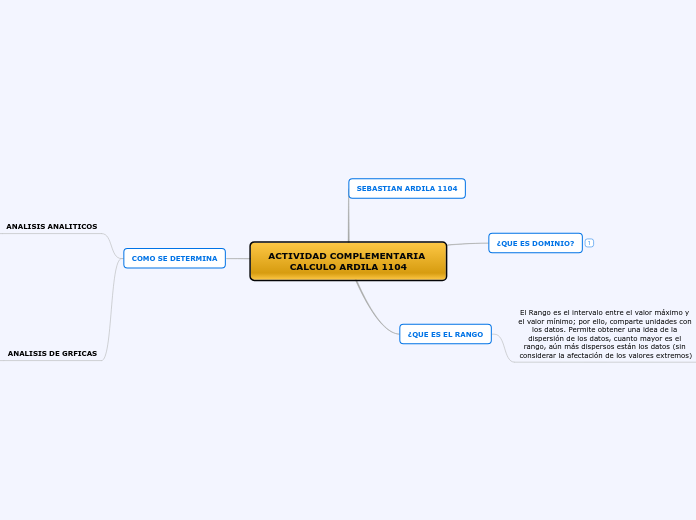
ACTIVIDAD COMPLEMENTARIA CALCULO ARDILA 1104

Még több ilyen

La Colonizacion de Asia y Africa

Szerző: Isai Arturo

CONCEPTOS QUÍMICOS

Szerző: isac zapata

FORMATOS TEXTUALES

Szerző: ANAIS ACHA POMAHUACRE

MAPA MENTAL

Szerző: luis yael sanchez

ACTIVIDAD COMPLEMENTARIA CALCULO ARDILA 1104

COMO SE DETERMINA

ANALISIS DE GRFICAS

-DOMINIO:Se analizan los valores del EJE X RANGO:Se analizan los valores del EJE Y -Se tienen en cuenta la represntacion de intervalos -Se identifica el tipo de funcion de acuerdo a la grafica

ANALISIS ANALITICOS

-Se identidica el tipo de funcion de acuerdo a la expresion algebraica -Se aplican las caracteristicas de solucion matematicas de acuerdo a la funcion como la inversa como la INVERSA DEUNA FUNCION -El dominio y rango de hallan analiticamente y se y se utilizan las nociones de INTERVALOS aplicadas a INECUACIONES. .

FUNCION CONSTANTE

Se llama asi a lo que no depende de ninguna variable y la podemos representar como una funcion matematica de la siguiente manera

f(x)=a

Donde a pertenece a los numeros reales y es una constante

FUNCION LOGARITMICA

Solo esta definida sobre los numeros positivos ,los numeros negativos y los 0 no tiene logaritmos. Esta funcion es la base reciproca a la exponencial de base a. Las bases mas usuales son de base 10 y base 2,718281...

f(x)= log 2x

FUNCION CUADRATICA

Su grafica es una curva llamada parabola cuyas caracteristicas son: Si a es mayor a 0 entonces e concava Si a es menor a 0 entonces es convexa

f(x)=ax² + bx + c

Donde a ,b y c son numeros reales.

FUNCION EXPONENCIAL

Es una funcion real que tiene la propiedad de que al ser derivada se obtiene la misma funcion ,toda funcion exponencial tiene por dominio todos los numeros reales.

f(x)=32ˣ

FUNCION LINEAL

Es aquella que satisface las siguientes dos propiedades ADITIVA:Si existen f(x) y f(y) entonces f(x+y) es lo mismo que f(x) y f(y). HOMOGENEA:f(ax)=af(x),para todo numero real a

f(x) = ax+b

Donde a y b son numeros reales.

¿QUE ES EL RANGO

El Rango es el intervalo entre el valor máximo y el valor mínimo; por ello, comparte unidades con los datos. Permite obtener una idea de la dispersión de los datos, cuanto mayor es el rango, aún más dispersos están los datos (sin considerar la afectación de los valores extremos)

¿QUE ES DOMINIO?

El Dominio de una función f (x) es el conjunto de todos los valores para los cuales la función está definida, y el rango de la función es el conjunto de todos los valores que f toma.

SEBASTIAN ARDILA 1104