Basic geometry and polygons
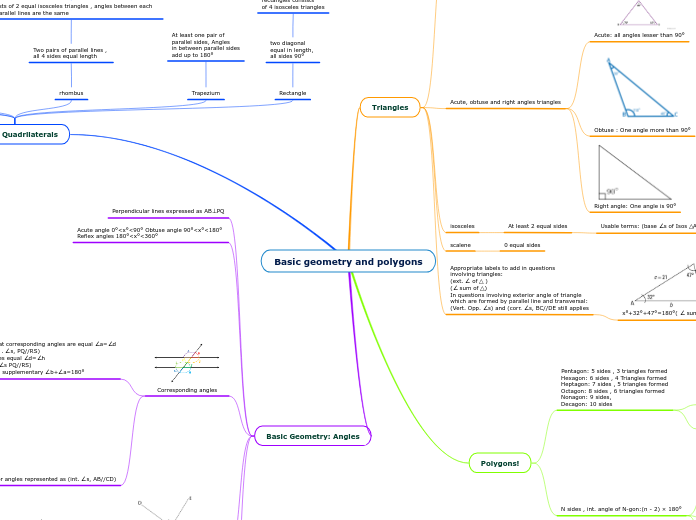
Basic Geometry: Angles
Vertically opposite angles occurs when straight lines intersect
A=B (vert. opp. ∠s)
Adjacent angles on a straight line,
Represented as (Adj. ∠s on a str. line)
180°= x + 3x + 2x (adj. ∠s on a str. line)
Corresponding angles
Interior angles represented as (int. ∠s, AB//CD)
This means that corresponding angles are equal ∠a=∠d
Example (Corr . ∠s, PQ//RS)
Alternate angles equal ∠d=∠h
Example (Alt. ∠s PQ//RS)
Interior angles supplementary ∠b+∠a=180°
This also consists of two pairs of parallel
lines . a line QP will have to be drawn horizontally in between
angle x in order to get two Z angles , where reflex of angle x
= w+z ( Alt.∠s , AA//QP) ( Alt ∠s CC//QP)
Example of corresponding angle question
where a=55° as alt. ∠s is applicable
Z angle can be applied to find the other
of corresponding angle
Acute angle 0°
Perpendicular lines expressed as AB⊥PQ
Special Quadrilaterals
Rectangle
two diagonal
equal in length,
all sides 90°
rectangles consists
of 4 isosceles triangles
Usable terms:Int. ∠ of rect.)
Trapezium
At least one pair of
parallel sides, Angles
in between parallel sides
add up to 180°
rhombus
Two pairs of parallel lines ,
all 4 sides equal length
Consists of 2 equal isosceles triangles , angles between each two parallel lines are the same
kite
At least 2 pairs of adjacent sides
consists of two isosceles triangles ,
one smaller than the other
∠DEA=∠DEC(longer diagonal BD bisects ∠ADC)
=25°
∠DEC°=90° ( diagonals of kite cut each other at
right angles)
∠BAD=∠BCD(opp. ∠s of kite)
parallelogram
Two pairs of parallel lines ,
diagonals bisect each other ,
angles in between add up to 180°
square
Polygons!
N sides , int. angle of N-gon:(n - 2) × 180°
Problem involving regular polygons with unknown no. of sides
Finding no. of sides using exterior angles of n-sided polygon
Sum of ext. angles=360°
Given size of each ext. angle: 24°
n=360°/24°=15
Finding no. of sides in regular polygon
if interior angle is given as°162°
(n-2)x180°/n= 162°
(n-2)x180°=162° x n
180n-162n=360
18n=360
n=20
Sum on int. angles in a decagon
Decagon:10 sides
Sum of int angles: (nx2)× 180°
Pentagon: 5 sides , 3 triangles formed
Hexagon: 6 sides , 4 Triangles formed
Heptagon: 7 sides , 5 triangles formed
Octagon: 8 sides , 6 triangles formed
Nonagon: 9 sides,
Decagon: 10 sides
exterior angle of a polygon
= 360 ÷ number of sides.
sum of interior angles
Pentagon:540°
Hexagon: 720°
Heptagon: 900°
Octagon: 1080°
Nonagon: 1260°
Decagon: 1440°
Formula :int. angle=(n - 2) × 180°
Triangles
Appropriate labels to add in questions
involving triangles:
(ext. ∠ of △ )
(∠ sum of △)
In questions involving exterior angle of triangle
which are formed by parallel line and transversal:
(Vert. Opp. ∠s) and (corr. ∠s, BC//DE still applies
x°+32°+47°=180°( ∠ sum of △)
scalene
0 equal sides
isosceles
At least 2 equal sides
Usable terms: (base ∠s of Isos △ABD
Acute, obtuse and right angles triangles
Right angle: One angle is 90°
Obtuse : One angle more than 90°
Acute: all angles lesser than 90°
Equilateral triangles
All angles are 60° , all sides equal length