a Hugo Fogue 5 éve
276
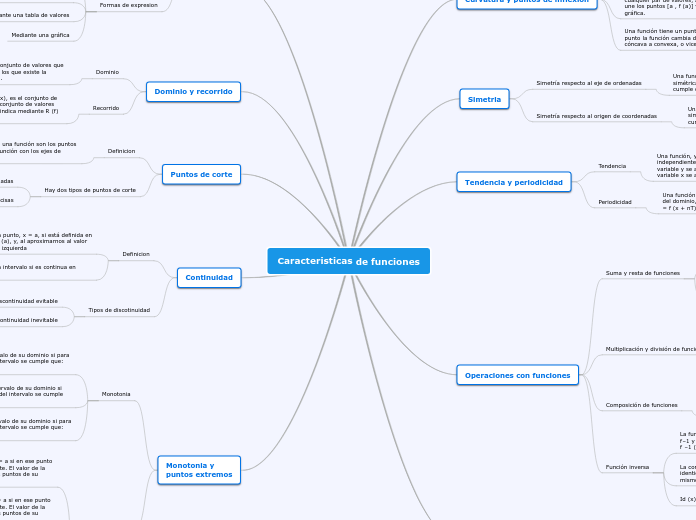
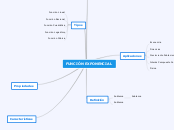
Caracteristicas de funciones
Las funciones matemáticas tienen varias características importantes que se pueden analizar desde diferentes perspectivas. Los puntos de corte, por ejemplo, son puntos de intersección de la gráfica de la función con los ejes de coordenadas y se dividen en puntos de corte con el eje de abscisas y el eje de ordenadas.