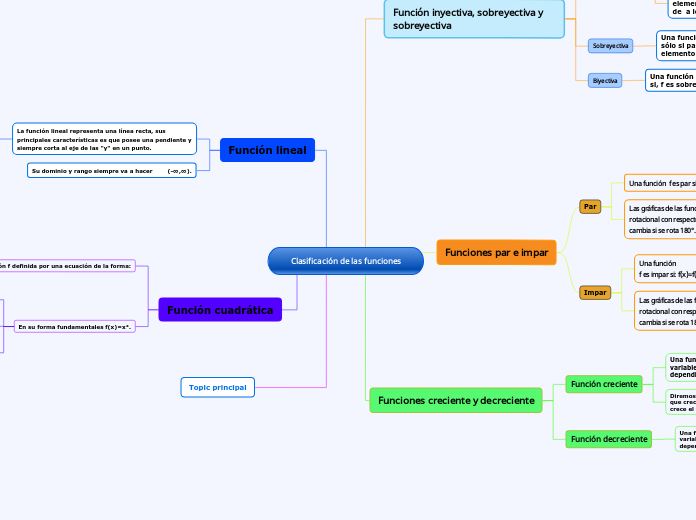
Clasificación de las funciones
In linguistics, syntax is the set of rules, principles, and processes that govern the structure of sentences in a given language, usually including word order.
Topic principal
Función cuadrática
A compound sentence is a sentence that has at least two independent clauses joined by a comma, semicolon or conjunction. An independent clause is a clause that has a subject and verb and forms a complete thought.
En su forma fundamentales f(x)=x².
Create your own compound sentences, using the coordinators above.
La función cuadrática siempre estará comprendida en el primer y cuarto cuadrante de una gráfica.
La función cuadrática forma una parábola simétrica con el eje vertical.
Una función cuadrática es un tipo de función que se caracteriza por ser un polinomio de segundo grado.
Una función f definida por una ecuación de la forma:
When independent clauses are joined with coordinators (also called coordinating conjunctions), commas and semicolons, they do more than just join the clauses. They add meaning and flow to your writing.
Donde a ≠ 0
y=f(x)= ax² + bx +c
Función lineal
A complex sentence is a sentence that contains an independent clause and one or more dependent clauses.
An independent clause can stand alone as a sentence, but a dependent clause even though it has a subject and a verb cannot stand alone.
Su dominio y rango siempre va a hacer (-∞,∞).
La función lineal representa una línea recta, sus principales características es que posee una pendiente y siempre corta al eje de las "y" en un punto.
Attributive clauses serve as an attribute to a noun (pronoun) in the main clause. This noun or pronoun is called the antecedent of the clause.
Su forma fundamental es: f(x)=X
Funciones creciente y decreciente
Función decreciente
See the example below and try to create your own simple sentences.
Tim is driving the red car.
Una función es decreciente cuando al aumentar la variable independiente x disminuye la variable dependiente y.
Función creciente
See the example below and try to create your own simple sentences.
Tim drives.
Diremos que una función es creciente cuando a medida que crece el valor de la variable independiente
crece el valor de la función.
Una función es creciente cuando al aumentar la variable independiente de x aumenta la variable dependiente y.
Funciones par e impar
Impar
Una función
f es impar si: f(x)=f(-x), ∀x
Par
An adverbial is an individual word (that is, an adverb), a phrase, or a clause that can modify a verb, an adjective, or a complete sentence.
Las gráficas de las funciones impares presentan simetría rotacional con respecto al origen. Es decir, la gráfica no cambia si se rota 180°.
Una función f es par si: fx=(-x), ∀x
Función inyectiva, sobreyectiva y sobreyectiva
Biyectiva
Traditional grammar defines the object in a sentence as the entity that is acted upon by the subject.
Una función f de A en B es biyectiva, si y sólo si, f es sobreyectiva e inyectiva.
The direct object is the receiver of the action mentioned in the sentence.
Sobreyectiva
The predicate of a sentence is the part that modifies the subject in some way. Because the subject is the person, place, or thing that a sentence is about, the predicate must contain a verb explaining what the subject does and can also include a modifier.
Una función f de A en B es sobreyectiva, si y sólo si para todoy perteneciente a B existe un elemento x perteneciente a A, tal que f(x)=y.
En otras palabras para que una función sea sobreyectiva, el condominio y la imagen deben coincidir.
Función inyectiva
The subject of a sentence is the person, place, thing, or idea that is doing or being something. You can find the subject of a sentence if you can find the verb.
Ask the question, 'Who or what 'verbs' or 'verbed'?' and the answer to that question is the subject.
Para que una función sea inyectiva, cada elemento del dominio puede debe ser imagen de a lo sumo un elemento del dominio.
Una función de A en B es inyectiva, si y sólo si, cualesquiera que sean x1 y x2 Є A, si X1 ≠ X2 entonces, f(X1) ≠ F(x2).