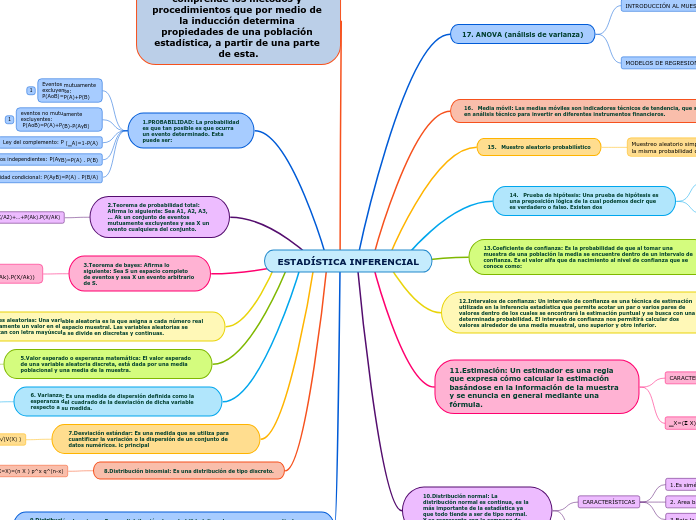
ESTADÍSTICA INFERENCIAL
9.Distribución de poisson: Es una distribución de probabilidad discreta que expresa, a partir de una frecuencia de ocurrencia media, la probabilidad de que ocurra un determinado número de eventos durante cierto periodo de tiempo.
P(X=X)=(μ^2 e^(-μ))/X!
8.Distribución binomial: Es una distribución de tipo discreto.
P(X=X)=(n X ) p^x q^(n-x)
7.Desviación estándar: Es una medida que se utiliza para cuantificar la variación o la dispersión de un conjunto de datos numéricos. ic principal
σ= √(V(X) )
6. Varianza: Es una medida de dispersión definida como la esperanza del cuadrado de la desviación de dicha variable respecto a su medida.
V(X)=σ^2=E(X^2 )-μ^2
5.Valor esperado o esperanza matemática: El valor esperado de una variable aleatoria discreta, está dada por una media poblacional y una media de la muestra.
E(x)=Ʃ X.P(X)
4.Variables aleatorias: Una variable aleatoria es la que asigna a cada número real uno o solamente un valor en el espacio muestral. Las variables aleatorias se representan con letra mayúscula se divide en discretas y continuas.
3.Teorema de bayes: Afirma lo siguiente: Sea S un espacio completo de eventos y sea X un evento arbitrario de S.
P(Ai/X)= (P(Ai).P(X/Ai)) (P(A1).P(X/A1)+P(A2).P(X/A2)+⋯+P(Ak).P(X/Ak))
2.Teorema de probabilidad total: Afirma lo siguiente: Sea A1, A2, A3, … Ak un conjunto de eventos mutuamente excluyentes y sea X un evento cualquiera del conjunto.
P(X)=P(A1).P(X/A1)+P(A2)P(X/A2)+…+P(Ak).P(X/AK)
1.PROBABILIDAD: La probabilidad es que tan posible es que ocurra un evento determinado. Esta puede ser:
Probabilidad condicional: P(AyB)=P(A) . P(B/A)
Regla del producto-Eventos independientes: P(AyB)=P(A) . P(B)
Ley del complemento: P (▁A)=1-P(A)
eventos no mutuamente excluyentes:
P(AoB)=P(A)+P(B)-P(AyB)
Eventos mutuamente excluyente: P(AoB)=P(A)+P(B)
Subtopic
Es una parte de la estadística que comprende los métodos y procedimientos que por medio de la inducción determina propiedades de una población estadística, a partir de una parte de esta.
10.Distribución normal: La distribución normal es continua, es la más importante de la estadística ya que todo tiende a ser de tipo normal. Y se representa con la campana de Gauss
F(x)=1/√(2π σ^2 ) e^(((x-μ)/σ)2)
3.Bajo la curva hay probabilidades
2. Area bajo la curva normal es igual a 1,0
1.Es simétrica
11.Estimación: Un estimador es una regla que expresa cómo calcular la estimación basándose en la información de la muestra y se enuncia en general mediante una fórmula.
▁X=(Ʃ X)/n
CARACTERÍSTICAS
2.Un estimador es eficiente si es insesgado y tiene mínima varianza.
1.Sesgo: Se dice que un estimador es insesgado si la media o el valor esperado de la distribución del estimador es igual al parámetro.
Insesgado S=√((Ʃ (X-〖X)〗^2)/(n-1))
Sesgado: S=√((Ʃ (X-〖X)〗^2)/n)
12.Intervalos de confianza: Un intervalo de confianza es una técnica de estimación utilizada en la inferencia estadística que permite acotar un par o varios pares de valores dentro de los cuales se encontrará la estimación puntual y se busca con una determinada probabilidad. El intervalo de confianza nos permitirá calcular dos valores alrededor de una media muestral, uno superior y otro inferior.
IC= ▁X ± Z . S/√n
13.Coeficiente de confianza: Es la probabilidad de que al tomar una muestra de una población la media se encuentre dentro de un intervalo de confianza. Es el valor alfa que da nacimiento al nivel de confianza que se conoce como:
NC=(1-α).100%
14. Prueba de hipótesis: Una prueba de hipótesis es una preposición lógica de la cual podemos decir que es verdadero o falso. Existen dos
Error tipo I: Se comete cuando rechazamos la hipótesis nula sabiendo que es verdadera. α
Error tipo II: Cuando aceptamos la hipótesis nula sabiendo que es falsa. Β
HO: Hipótesis nula
HA: Hipótesis alternativa o del investigador
15. Muestro aleatorio probabilístico
Muestreo aleatorio simple: Todos los individuos tienen la misma probabilidad de ser elegidos.
Sin reemplazo: “No puede volver a participar”
Con remplazo: “Puede volver a participar”
16. Media móvil: Las medias móviles son indicadores técnicos de tendencia, que se utilizan en análisis técnico para invertir en diferentes instrumentos financieros.
17. ANOVA (análisis de varianza)
MODELOS DE REGRESION
Examinal y logaritmica
Lineal Múltiple
Lineal (Mínimos cuadros)
INTRODUCCIÓN AL MUESTREO
MAC
MAE
MAS
