a ILVER CIFUENTES 3 éve
162
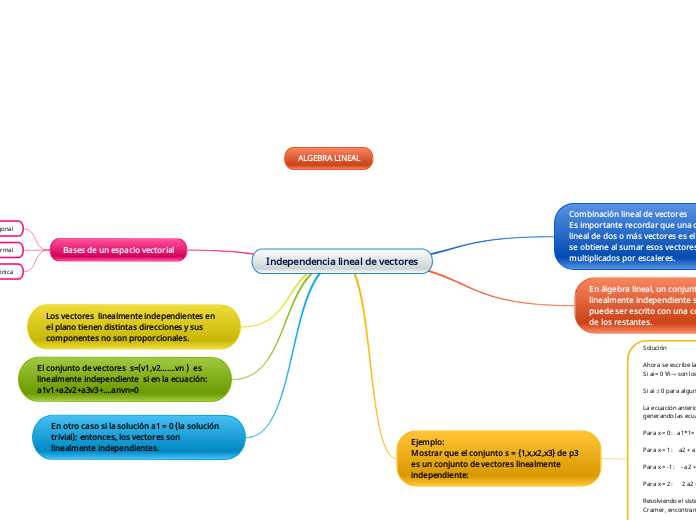
Independencia lineal de vectores
En el estudio de álgebra lineal, un concepto fundamental es la independencia lineal de vectores. Un conjunto de vectores se considera linealmente independiente si ninguno de ellos puede expresarse como una combinación lineal de los otros.