a DANIEL CAICEDO DUARTE 3 éve
178
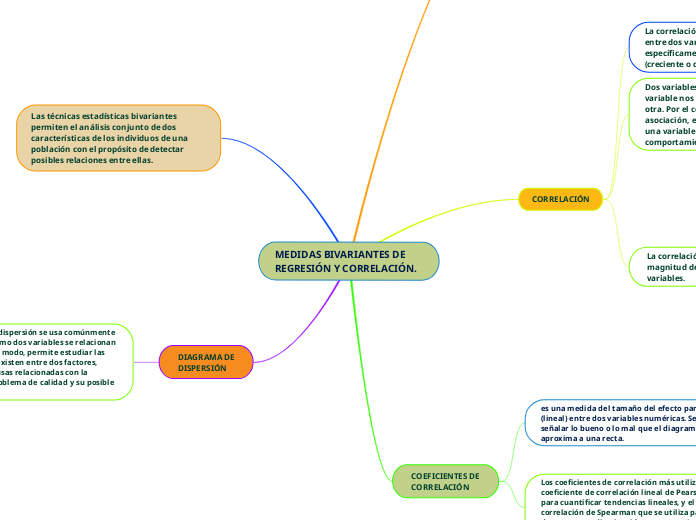
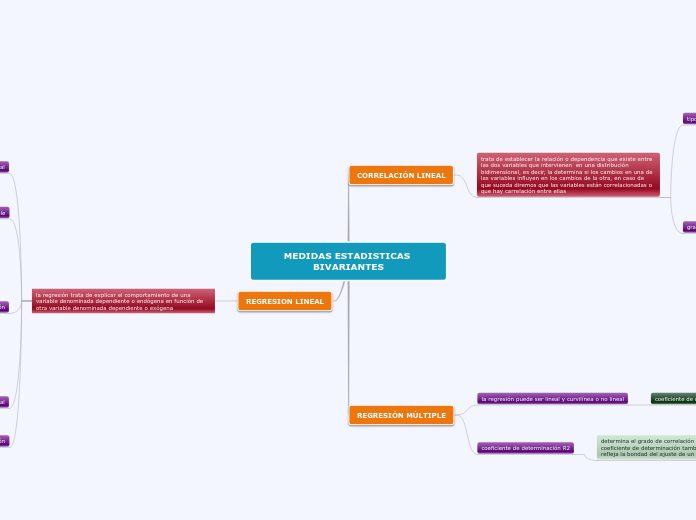
MEDIDAS BIVARIANTES DE REGRESIÓN Y CORRELACIÓN.
La regresión y la correlación son herramientas estadísticas esenciales para analizar la relación entre dos variables. La regresión lineal simple se enfoca en explicar cómo una variable dependiente se ve afectada por una variable independiente.